动画
将3维模型和2维图片延申到时间的维度,按照顺序和一定的频率播放图片
- 电影:24帧
- 视频:30帧
- 虚拟现实:90帧以上
关键帧插值
关键帧:即人物动作发生转变的一帧动画
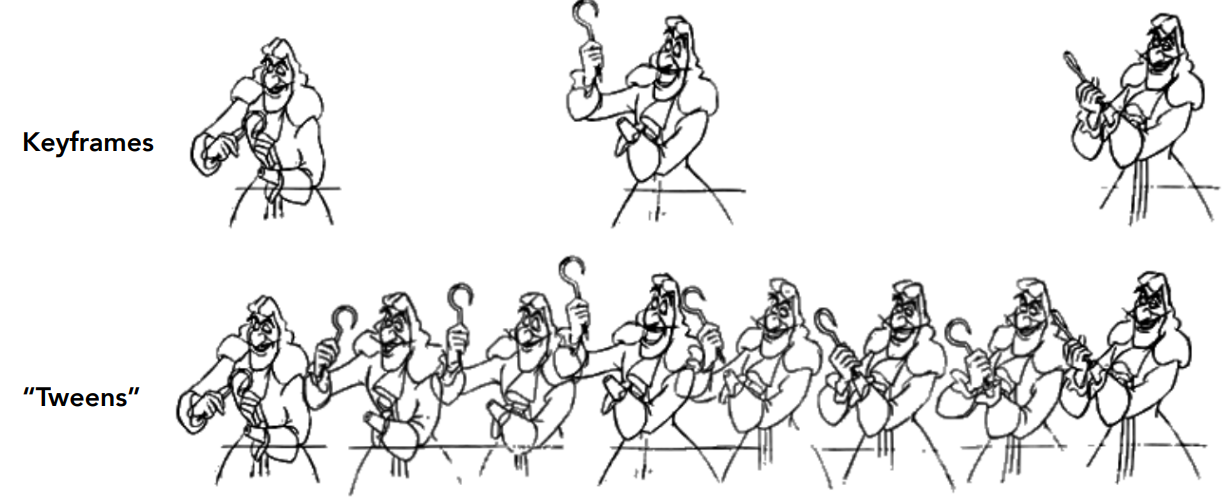
关键帧插值一般使用插值的方法来进行补帧,将每一个关键帧当作参数值的向量
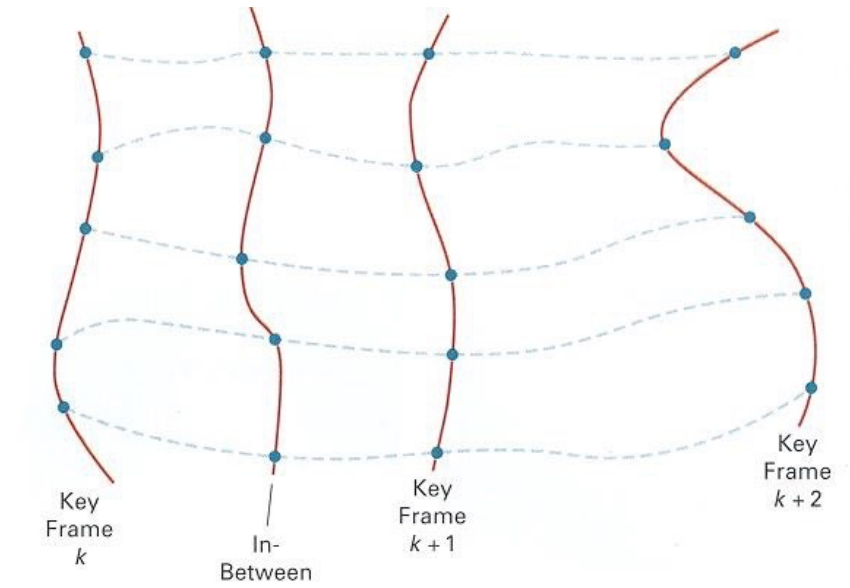
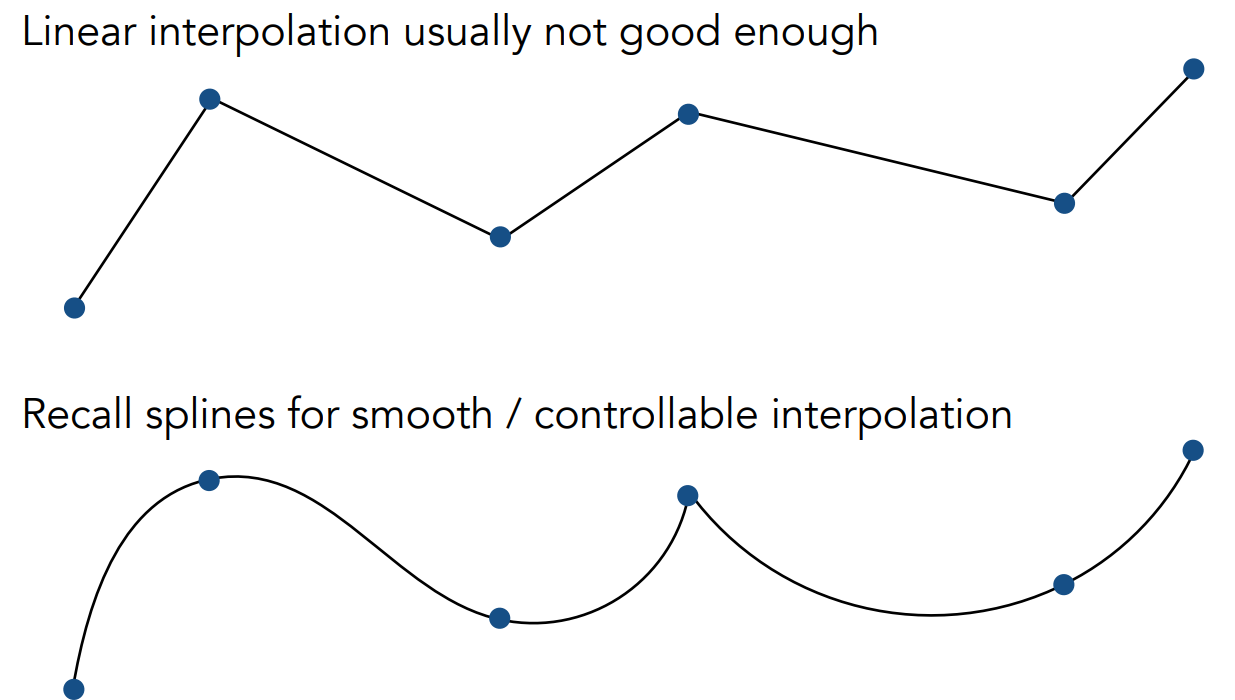
但是线性插值的效果并不够好,可以用平滑可控插值的回归样条
物理仿真
根据牛顿第二定律,使用数值模拟生成物体的运动
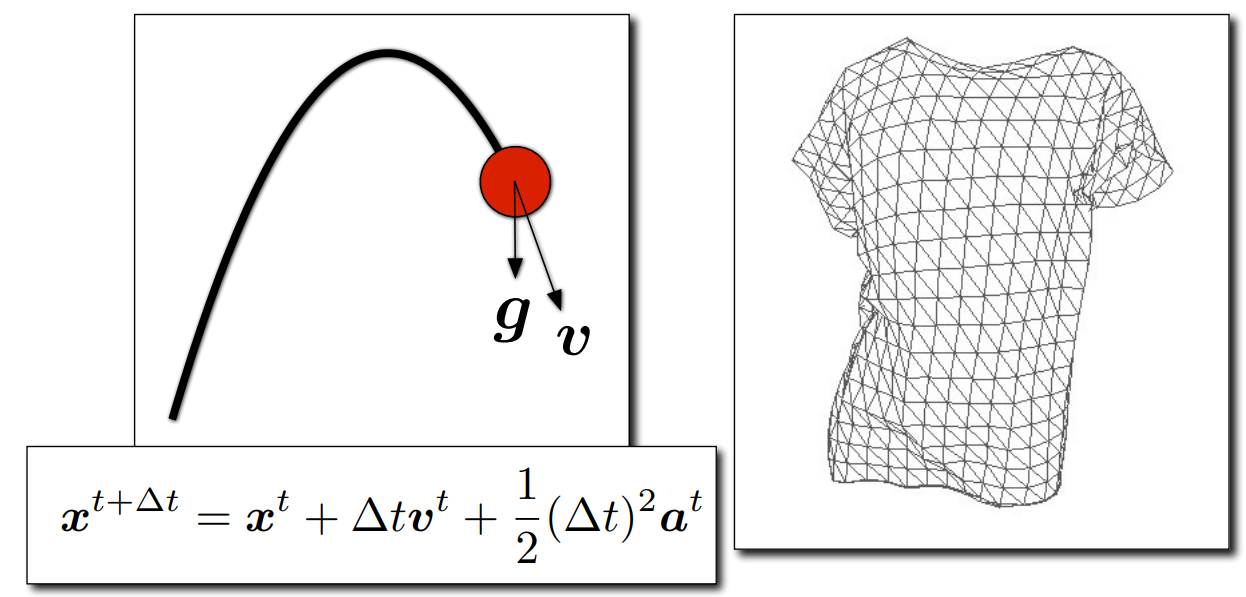
质点弹簧系统
从理想化弹簧开始,没有长度,作用力会导致位移

加入弹簧原长对振子的影响
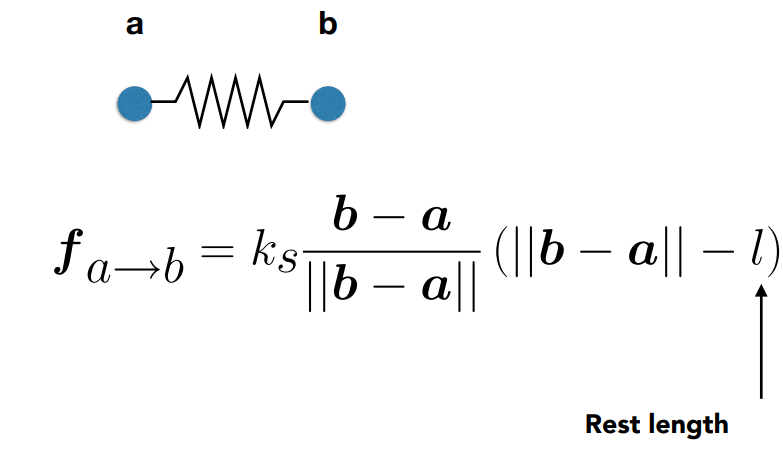
继续加入能量衰减的部分

再加入内部阻尼模拟

通过弹簧之间结构的连接可以决定一个图形的行为
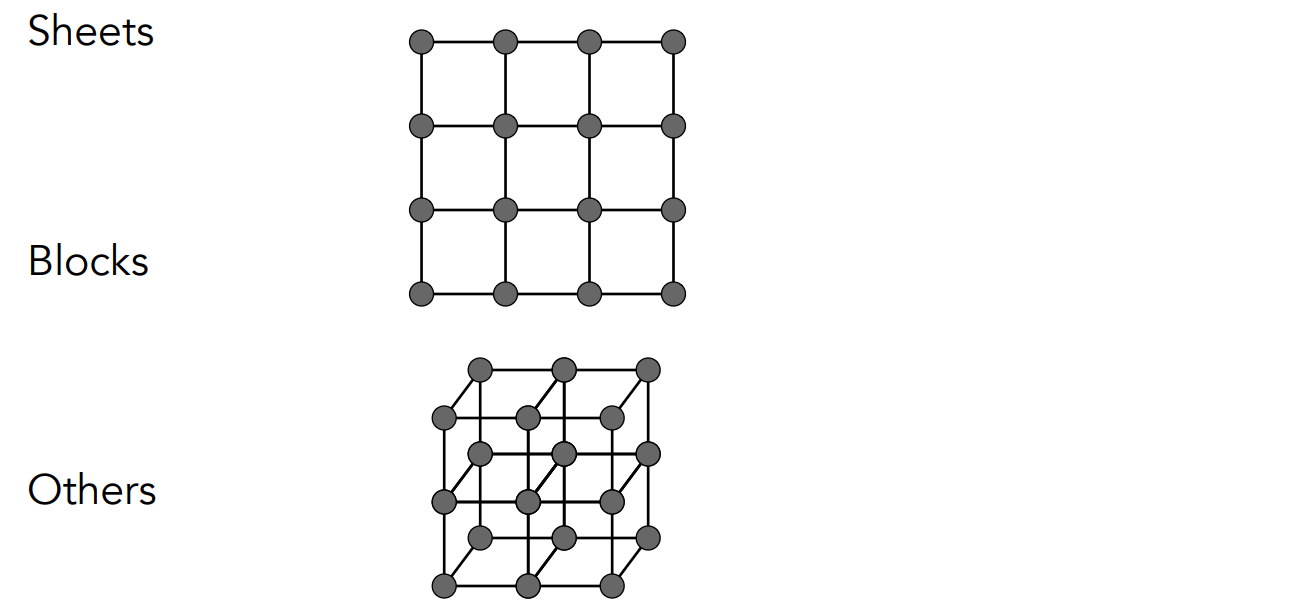
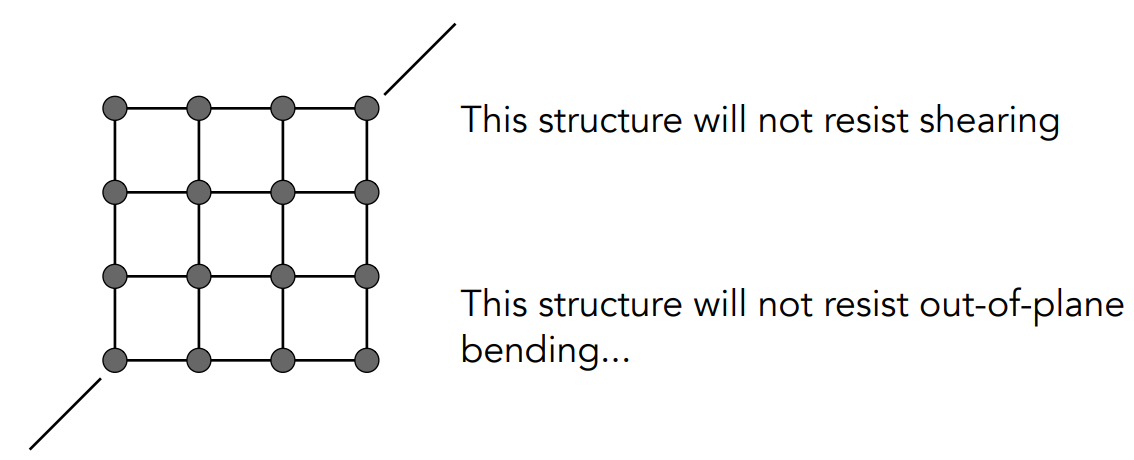
用上图的方式来模拟布料,但是无法正确表示切变的影响,会使原来的形状不在同一个平面上,进行改进

还可以采用一种有限元方法,用来做汽车碰撞,主要思想是力与力之间的传导
粒子系统

主要思想:
- 将动态的系统建模为大量粒子的集合
- 每个粒子的运动都是由一组物理力定义的
- 具备可扩展性,粒子越少,速度越快;粒子越多,速度越慢
步骤:
- 创建新的粒子
- 计算每个例子的力
- 更新每个粒子的位置和速度
- 移除死掉的粒子
- 渲染粒子
粒子系统的作用力:
- 引力和斥力:万有引力,电磁力,弹力,推进力
- 阻力:摩擦力,空气阻力,粘滞力
- 碰撞:与墙壁,容器,固定的物体发生碰撞
模拟动物集群
- 将这些动物建模成一个粒子
- 每个粒子只受简单的力
- 使用数值方式模拟大粒子系统的演化
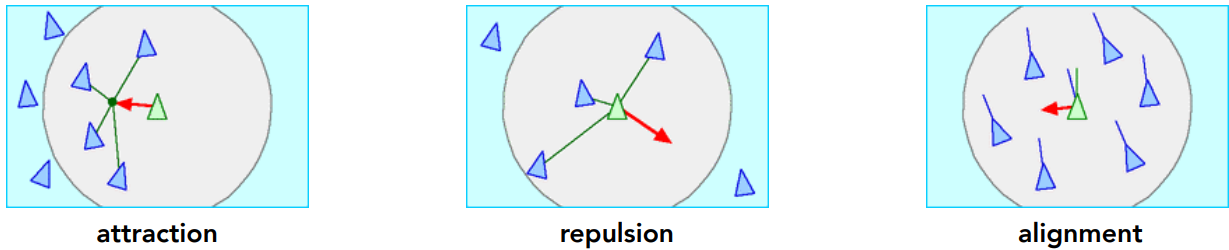
根据这些粒子的行为模式可以分为三类:
- attraction:融入周围的其他粒子
- repulsion:相互排斥
- alignment:考虑运动的平均方向
运动学
模拟生物运动的方式
正运动学
通过各种关节骨骼的运动算出各部分的摆放位置
关节骨骼系统
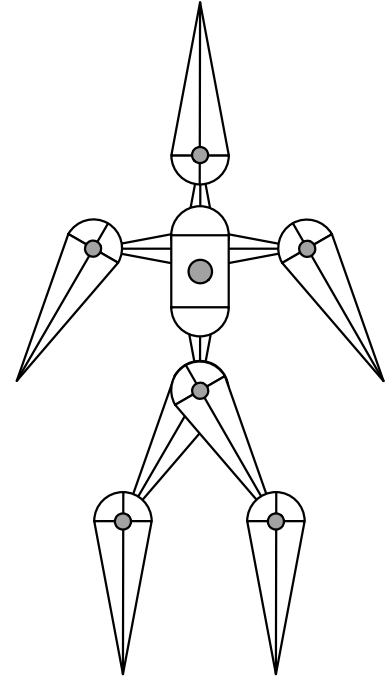
通过简单的形体来描述一种拓扑结构与关节间的关系,本身会形成一种良好的树形结构,便于加速
旋转类型
有三种旋转类型
Pin:在平面内旋转
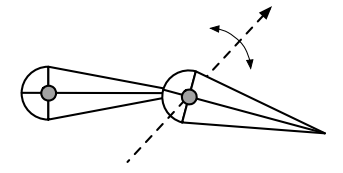
Ball:可以旋转到不同平面
Prismatic:拉长
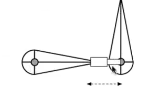
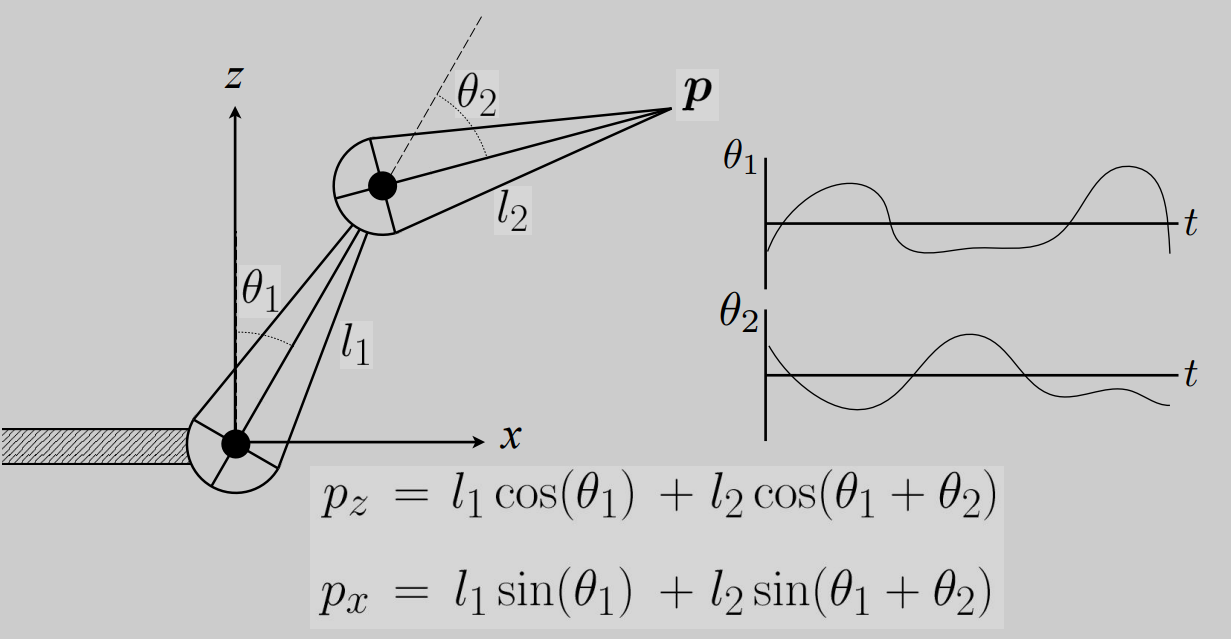
逆向运动学
考虑正向运动学的一些缺点:动画难以用物理的方式实现,不便于动画师的制作
因此考虑逆向运动学:知道末端的位置后计算出关节和骨骼应该如何摆放
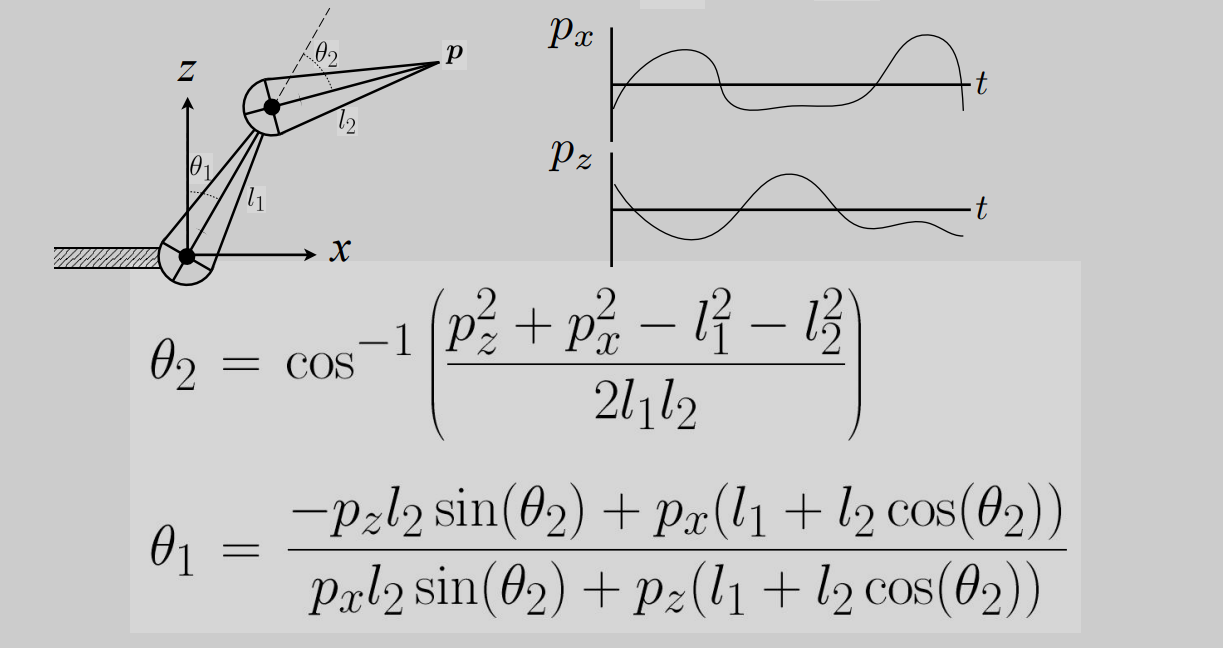
但是逆向运动学的解不唯一,且解有可能不存在
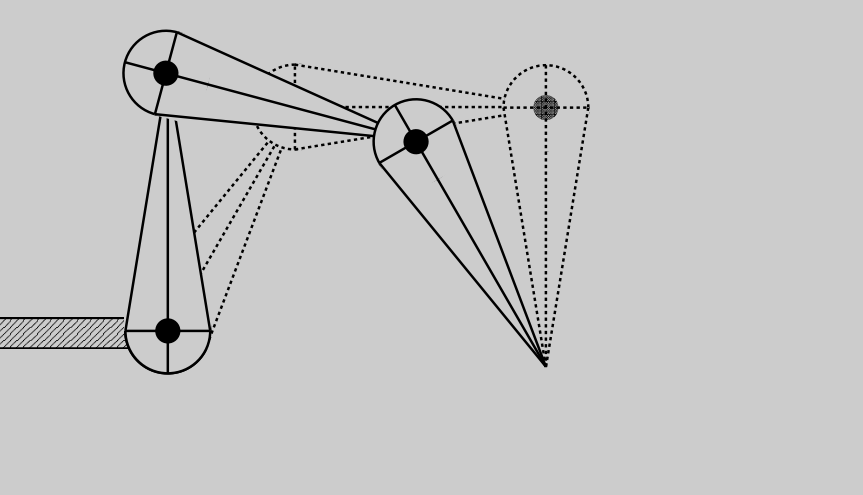
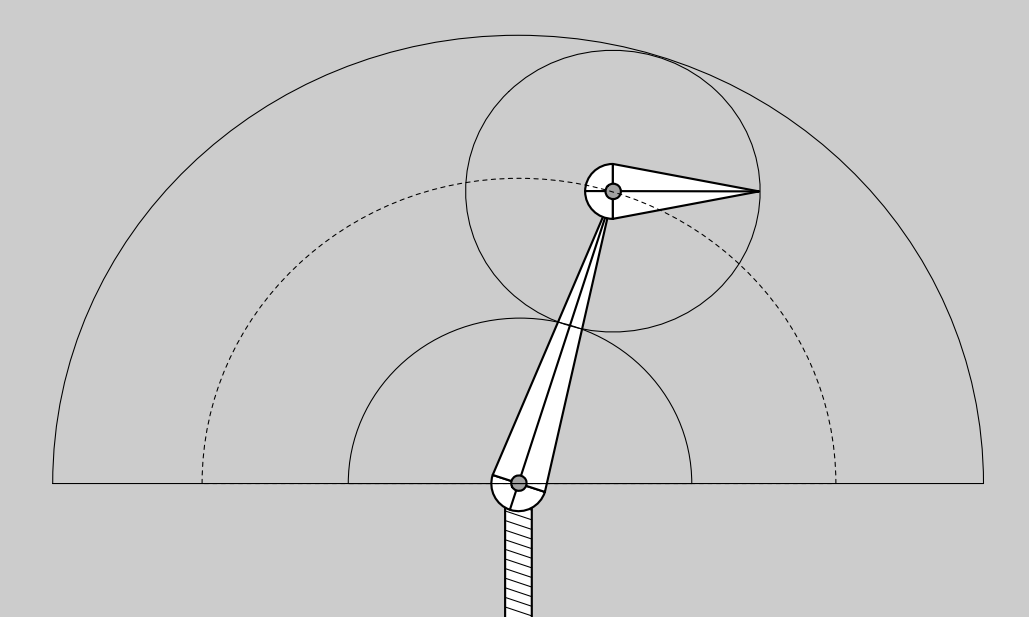
一些解决方案:
- 选择一个初始构型
- 定义一个误差度量(如:目标与当前位置之间距离的平方)
- 计算误差梯度作为构型的函数
- 应用梯度下降法
绑定
对物体表面的各个点进行建模方面的绑定,允许更快速直观地修改姿势,变形和表情

形状混合
直接在曲面之间进行插值
简单的方案:取顶点位置的线性组合,样条用于控制随着时间的推移权重的选择

动作捕捉
直接通过设备对真人的动作进行采样

动画制作管线

单个粒子模拟
研究一个粒子的运动然后泛化到大多数粒子
单个粒子的运动
认为粒子的运动由速度场决定,这个速度场是一个关于位置和时间的函数
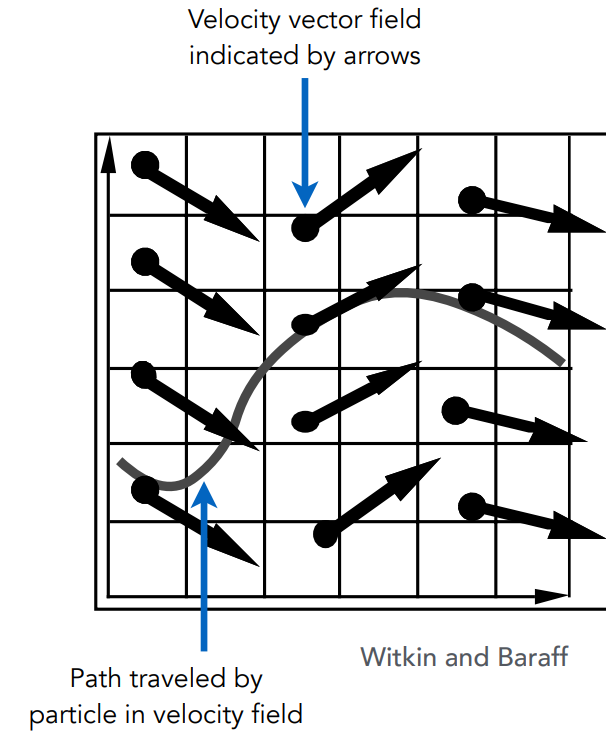
计算粒子的位置需要解一个一阶的常微分方程
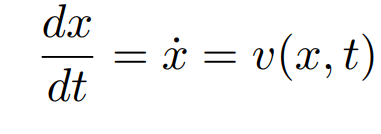
欧拉方法
欧拉方法是一种简单的迭代方法用于求解给定初始位置和速度场的点经过时间t后所处的位置
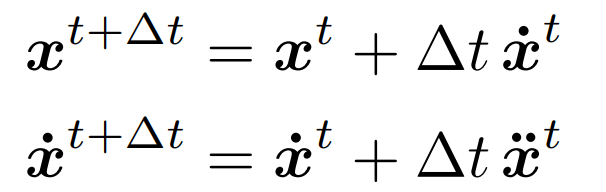
等式右边所用到的都是上一帧的参数,左侧是计算得到的下一帧的值
但是使用欧拉方法不太稳定,会产生较大的误差
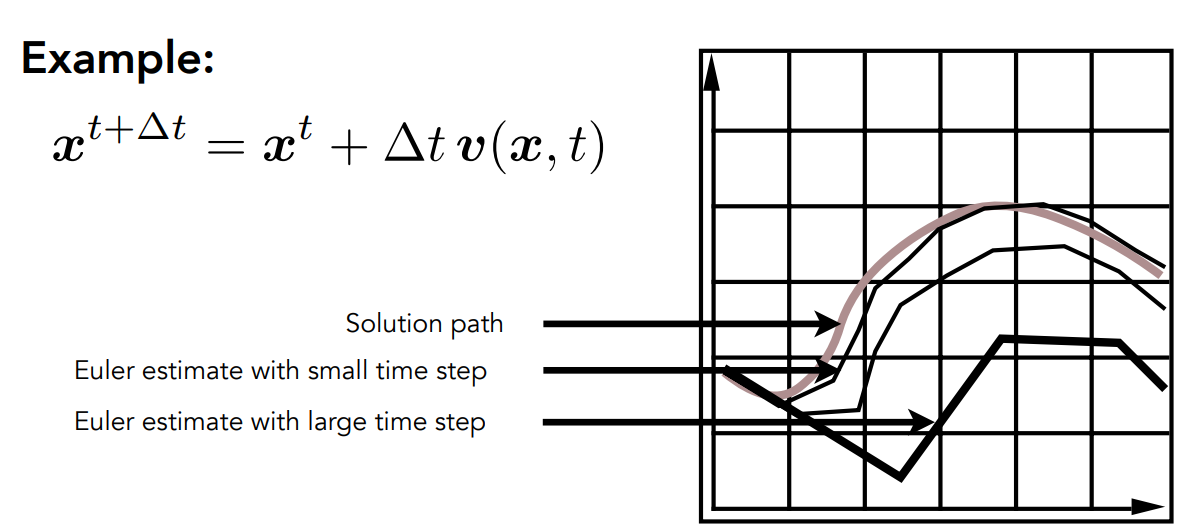
并且欧拉方法不稳定,不能始终沿着指定的轨迹运动
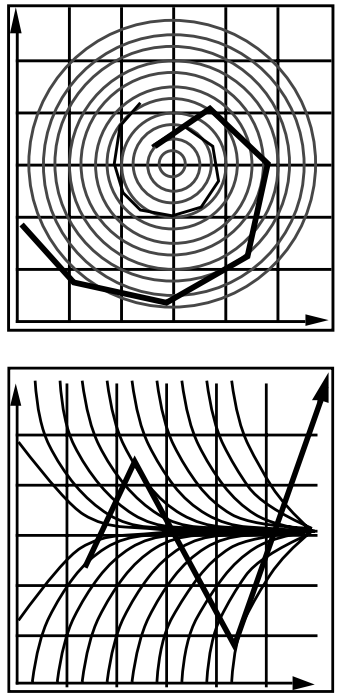
克服不稳定性的方法
误差可以通过减小
中点法
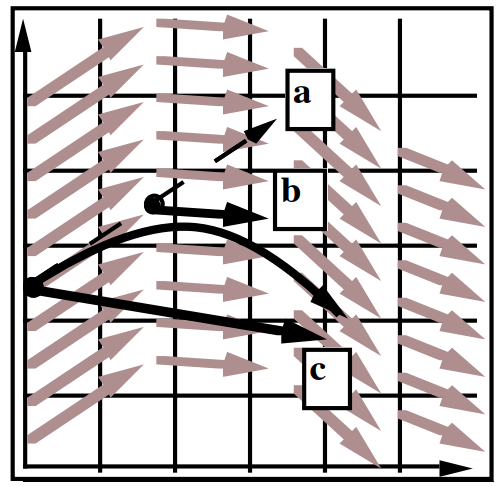
- 使用欧拉方法计算,到达点A
- 使用欧拉方法计算起始点到A点的中点B的方向
- 从起始点向这个方向走到C
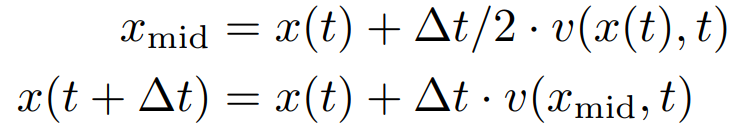
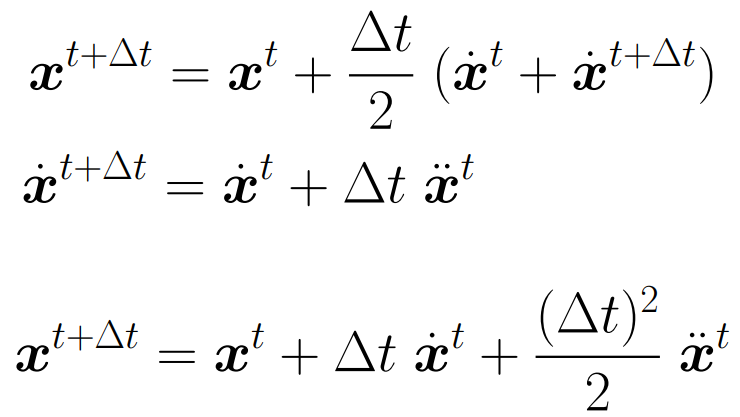
自适应步长法
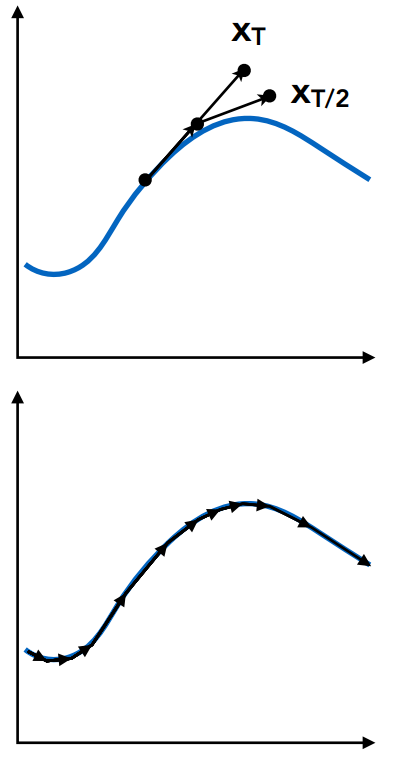
- 使用步长为T的欧拉方法计算到达
- 再次用一半的步长计算得到
- 比较误差,选取对应所需要的步长
- 重复上述步骤
隐式欧拉方法
也称为后向欧拉方法,通过后一帧的参数来计算当前帧的位置
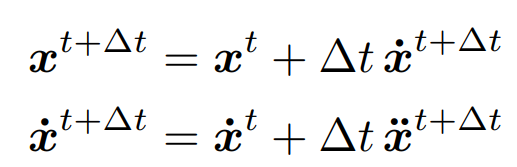
但是这个方程是非线性的,可以采用Runge-Kutta Families(龙格-库塔法)方法进行计算
最常用的就是RK4,四阶的Runge-Kutta法

量化稳定性的方法:
- 使用局部截断误差/总截断累计误差来研究稳定性
- 研究误差的阶
- 隐式欧拉方法的阶数为1,局部阶段误差为
,全局截断误差为
基于位置/韦尔莱积分法
一种不基于物理的方法,通过调整物体的位置使得物体满足某种性质
- 在修改欧拉前步之后,约束粒子的位置以防止不稳定的现象
- 使用约束位置计算速度
- 这两种思想都会耗散能量,使其具有稳定性
快速,简单但不满足能量守恒
刚体模拟
刚体模拟与模拟单个粒子相似,只需要考虑一些属性
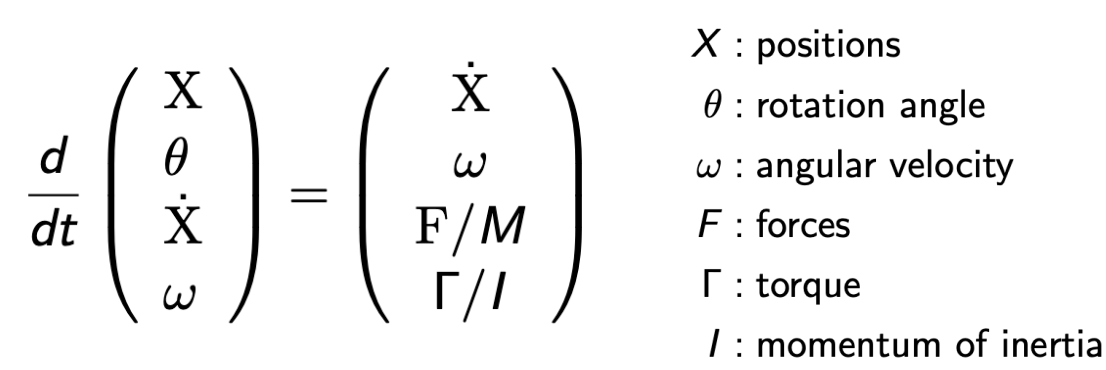
流体模拟
流体比刚体更为复杂一点
基于位置的模拟

可以用到上述提到的基于位置的模拟方法:
- 认为水由刚体小球组成
- 认为水是不可压缩的
- 只要某处的密度发生改变,通过粒子的位置纠正
- 需要知道任何位置的密度梯度
- 使用梯度下降法更新
质点法与网格法
质点法:跟踪同一个质点
网格法:观察同一个位置不同时间的图像
物质点法(MPM,Material Point Method)
一种结合质点法与网格法的方法

- 认为粒子带有材质属性
- 使用网格来做数值积分
- 粒子将属性传递给网格,网格执行更新
- 插值回粒子