在进行了光栅化之后,已经可以将

着色模型

在着色时我们可以将物体大致分为三部分:
- 高光部分(近似发生镜面反射的部分)
- 漫反射部分(物体表面光照基本均匀的部分)
- 环境光照部分(经过多次反射后到达物体表面)
着色局部性
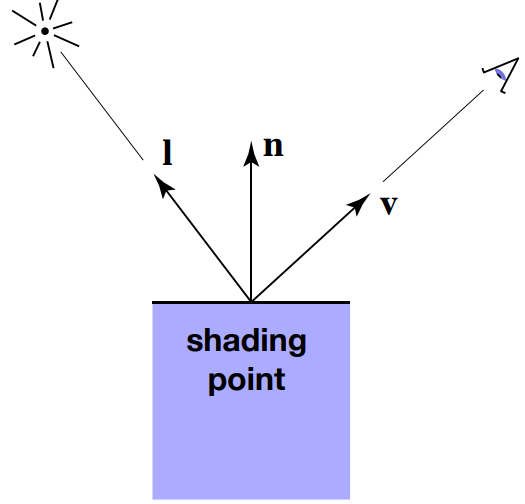
在进行着色的计算时,我们会分析光线照射到物体表面的每一个点,称为着色点,对于每个着色点将其视为一个微平面构建法线
发现着色的最终结果受以下几个因素的影响:
- 观测方向
- 表面法线方向
- 光照方向
- 表面的属性参数:颜色,材质等
着色时仅考虑光照对物体表面的影响,不考虑其他物体的阴影对物体本身的影响
布林-冯着色模型
由前可知,着色大致可分为三部分:漫反射,高光反射,环境光反射,下面学习每一部分具体如何实现
漫反射
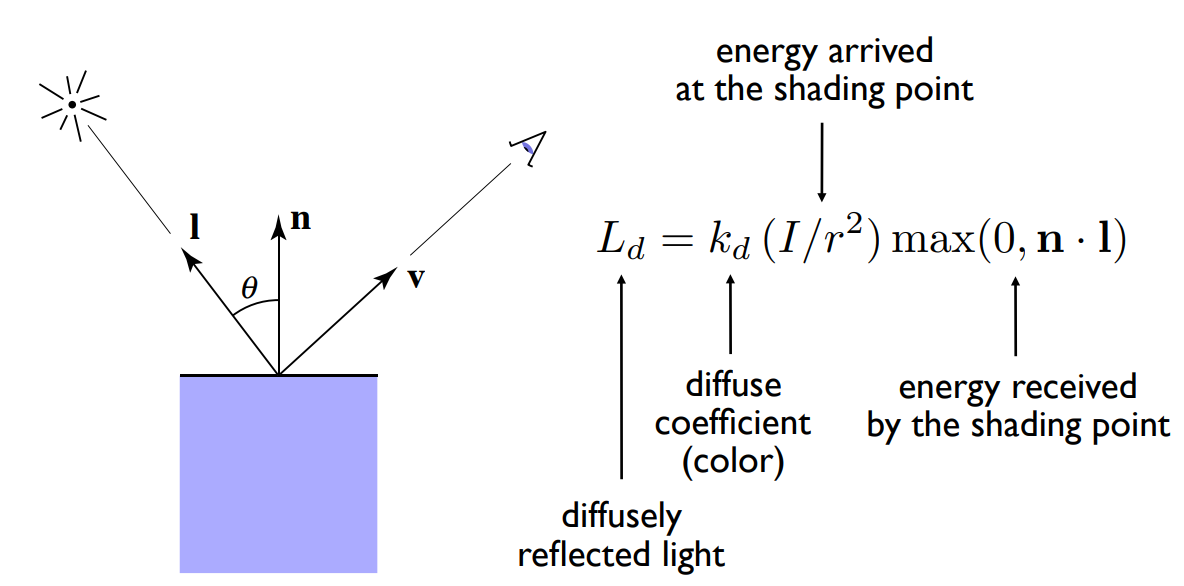
当光线照射到一个点时,光线会向各个方向发生反射,漫反射的反射光强主要受到光照角度、光照强度、漫反射系数等因素的影响,而与观测角度没有关系,在各个方向所观察到的现象大致相同
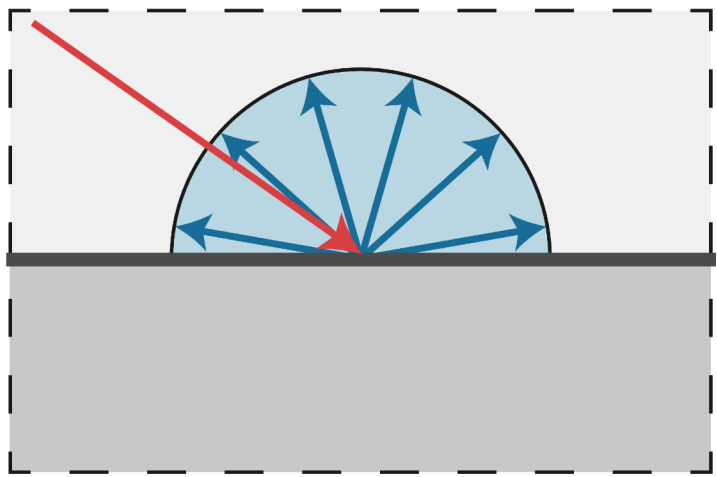
兰伯特余弦定理
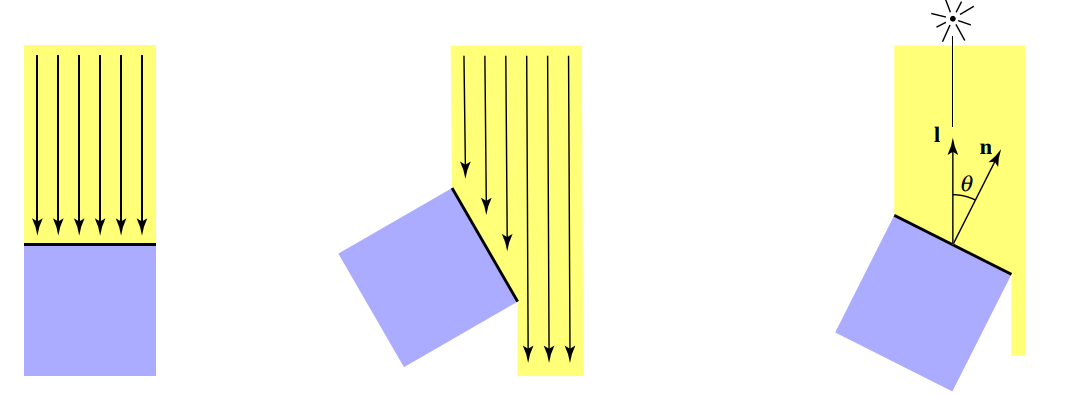
由该定理可知,物体表面所接收到的光照能量与光照角度相关,有公式:
光照衰减
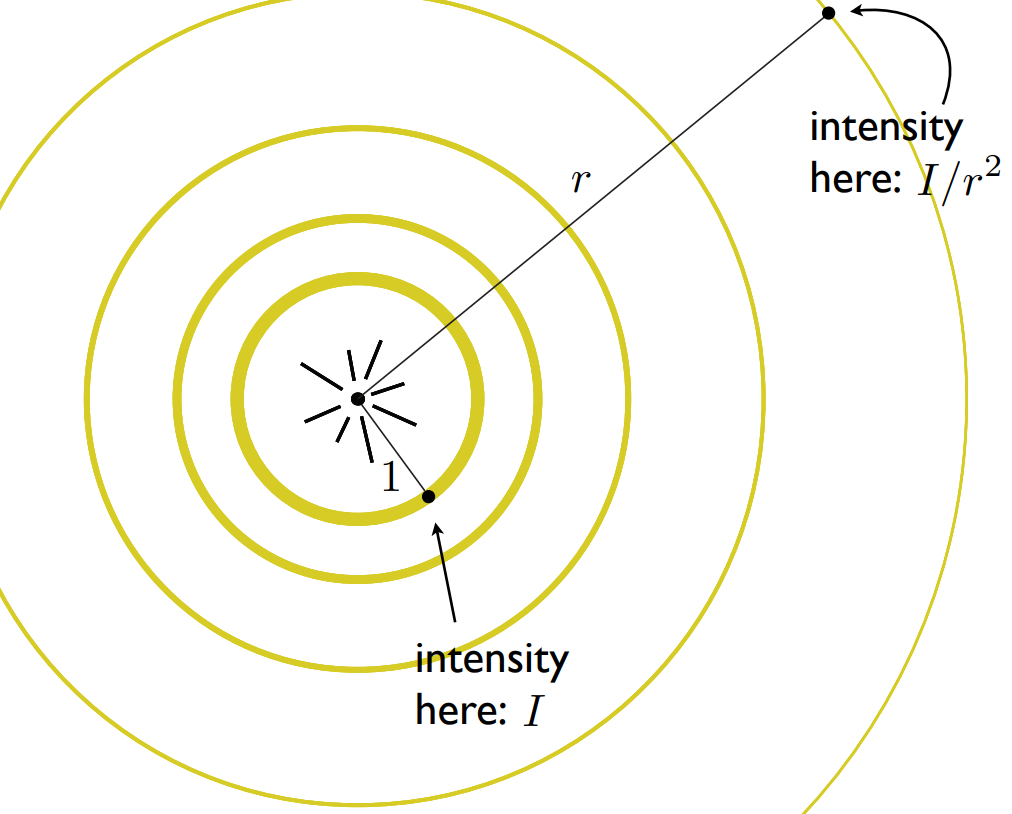
光在传播时,随着距离的增加,光照的能量会发生衰减
如果规定单位长度处的光照能量为:
漫反射系数

不同的材质具有不同的漫反射系数
漫反射公式
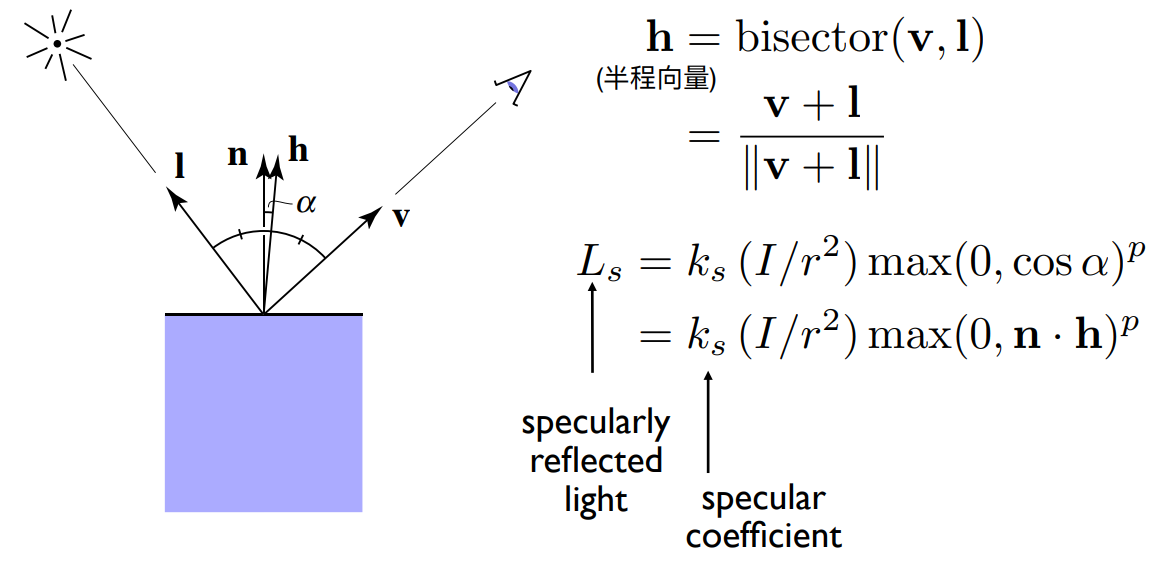
高光反射
当物体表面发生近似于镜面反射的反射情况时,我们在某个特定的角度附近观测时即可看到高光现象
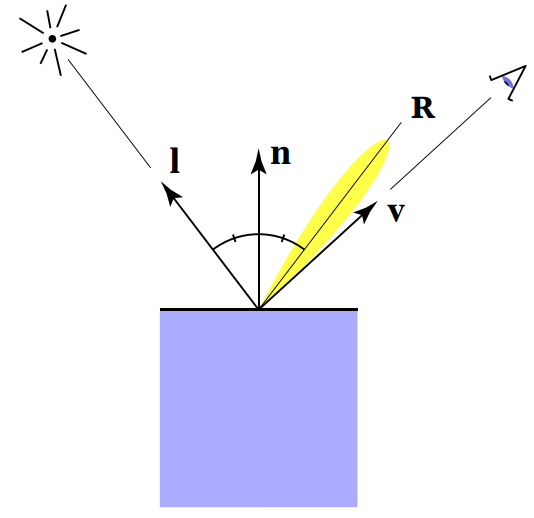
高光区域
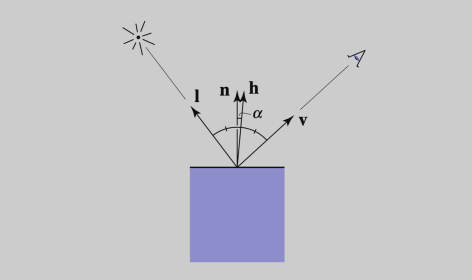
如何计算这个特定的角度?此时引入一个新的向量,称为半程向量
然后可以利用半程向量与法向量计算两者的夹角
高光突变
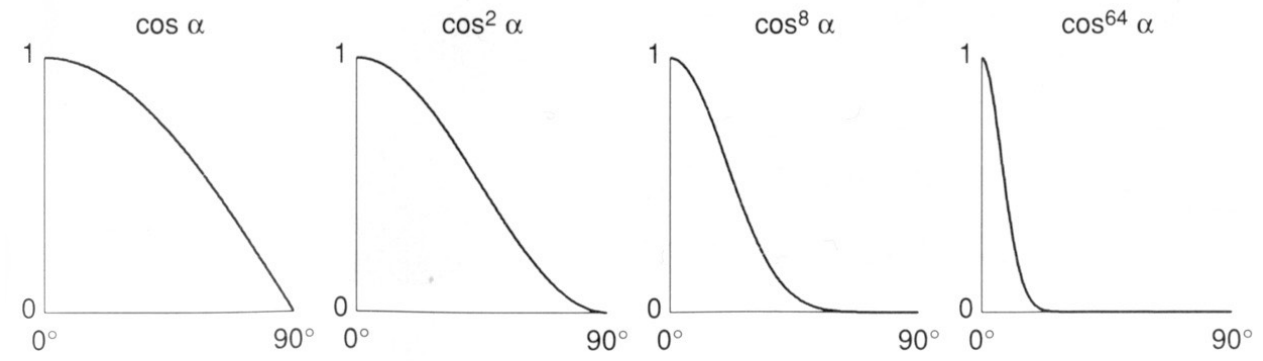
当仅用
高光系数

与漫反射系数一样,可以用一个高光系数
由这一张图可以看出,
高光反射公式
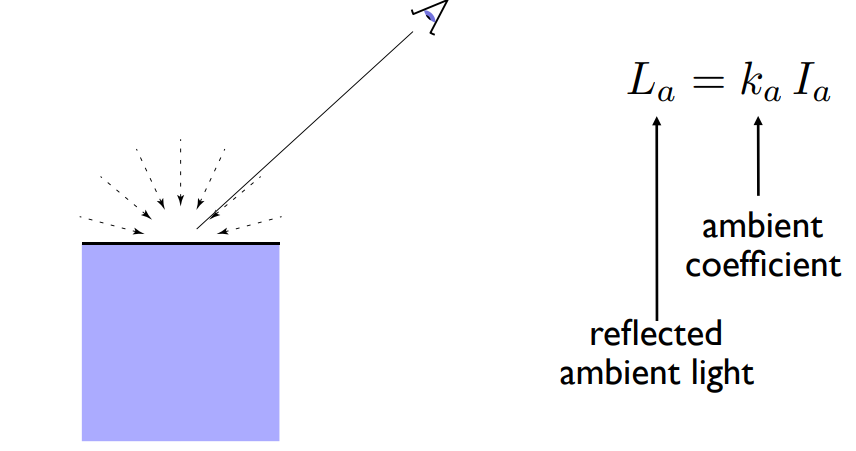
环境反射
在
光照公式
将上述的三部分相加,所得到的和,即为布林-冯模型所得到的着色公式

着色频率
在得出着色公式时,考虑的是每个点的情况,而在实际处理中考虑每个点会造成极大的性能开销,因此根据采样方式的不同也即着色频率的不同划分出三种着色方式:
- 平面着色(
) - 顶点着色(
) - 像素着色(
)

平面着色

将物体表面划分成一个个的三角形或四边形,然后对每一个平面进行着色即可
法向量即为平面的法向量,通过平面的两条边进行叉乘即可得出
顶点着色

同样将物体以三角形划分,此时对于三角形的每一个顶点进行着色
基于三角形每个顶点的着色,三角形内部的点通过插值计算实现平滑过渡
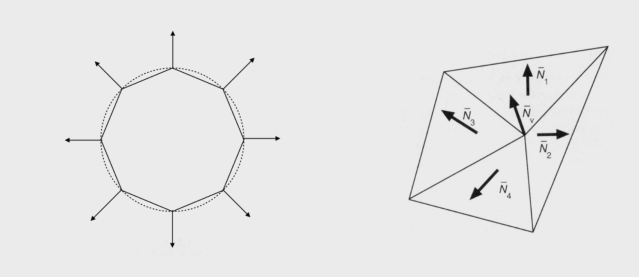
顶点的法向量则通过本身的几何形状或者一个点周围的四个平面的法向量的平均值得出
像素着色

直接对于每一个像素进行着色
对于每一个像素利用三角形的三个顶点的法向量进行重心插值得到其法向量
比较
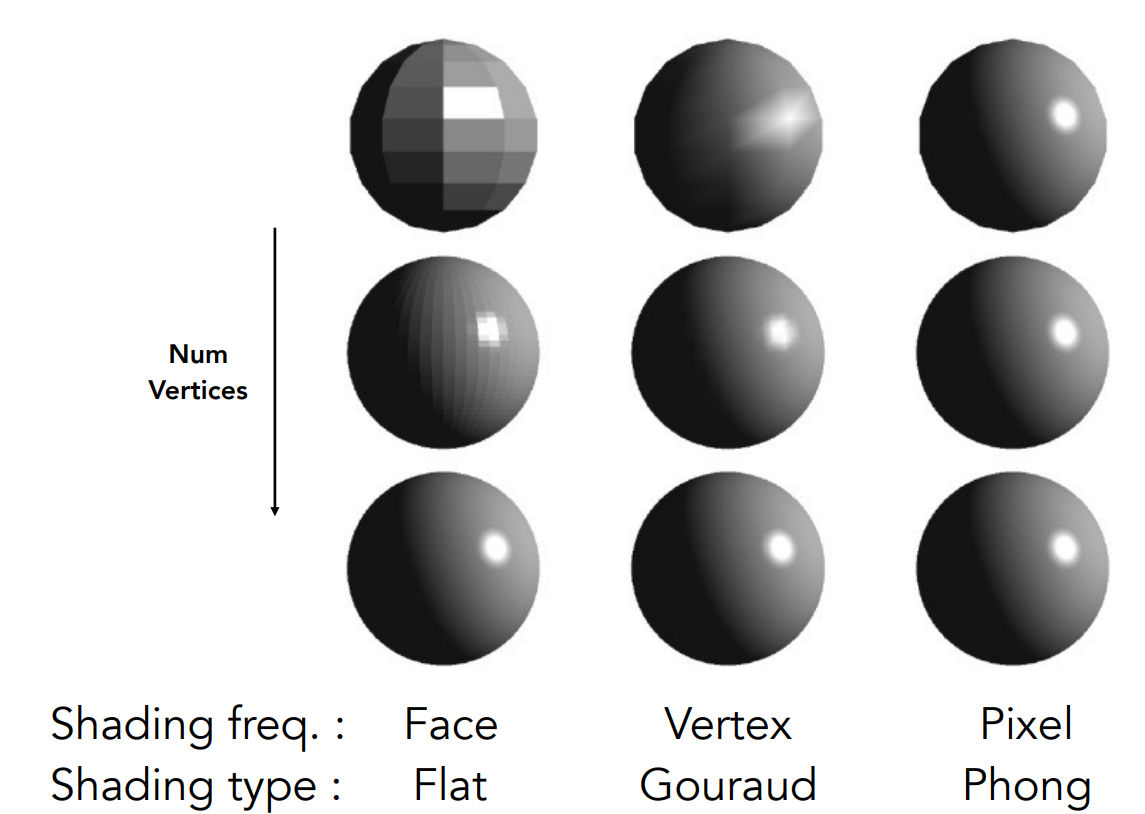
通过比较发现,三种着色方式本身并没有优劣之分,区别在于细分的程度,划分的越细,效果越好,三者的效果越接近
渲染管线
渲染管线:将图像由
可分为五个阶段:
- 顶点处理
- 三角形处理
- 光栅化
- 片元处理
- 帧缓冲操作
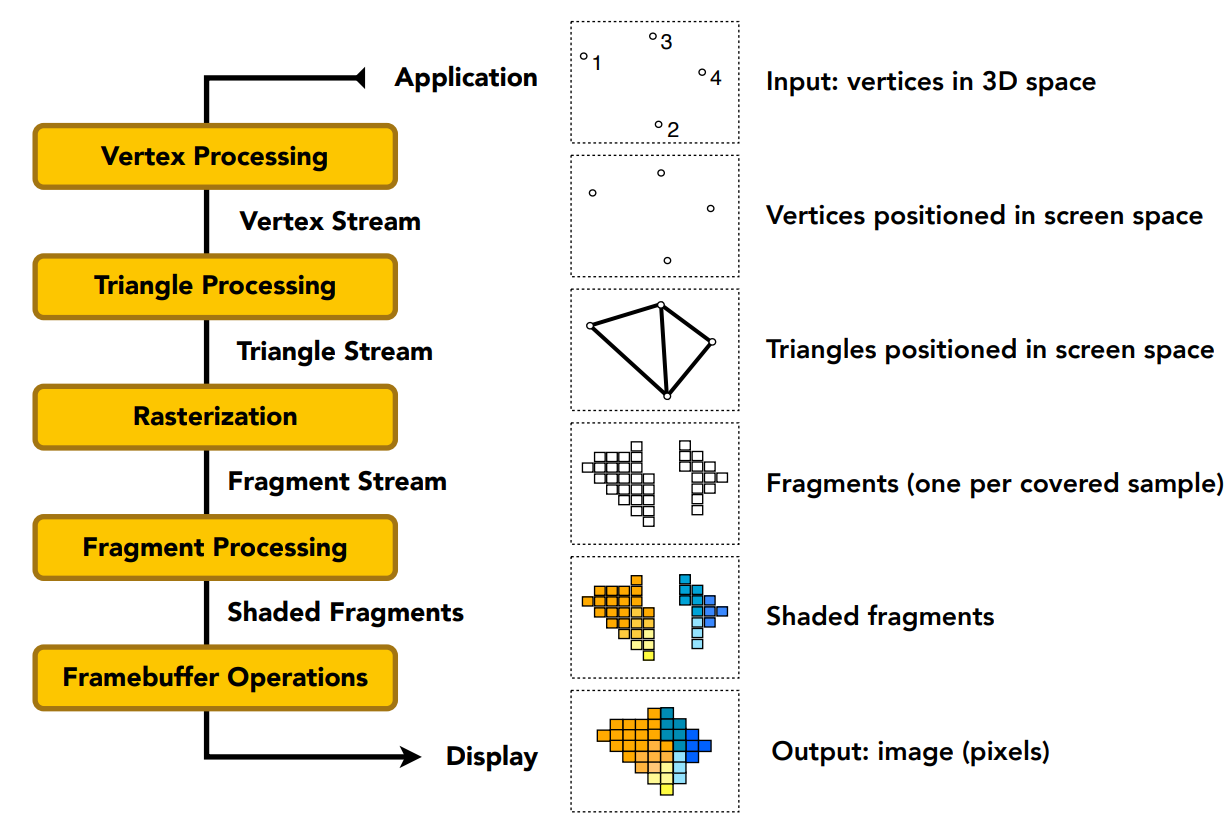
顶点处理
将一个三维模型通过细分,转换成一个个三角形的近似,然后将这些三角形顶点的坐标,通过
三角形处理
将经过变换后的定点坐标重新连线,装配成一个个的三角形,便于之后进行光栅化
光栅化
对得到的连续的二维图像进行采样,转换成离散的二维图像,对应到屏幕上的每个像素
在这个阶段会发生走样的问题,解决方式详见上一节
片元处理
对每个片元进行颜色,纹理,深度的计算,其间运用到大量插值的方法
帧缓冲操作
对片元进行颜色混合,模板测试,深度测试,透明度检查等一系列操作,将最终结果保存在帧缓冲区,显示器定时读取帧缓冲区,将内容呈现在屏幕上
关于着色
粗略划分,一条完整的渲染管线分为三部分:顶点处理,光栅化,着色
根据着色频率的不同,着色行为会发生在不同的阶段:
- 顶点着色:发生在顶点处理阶段
- 像素着色:发生在片元处理阶段
在现代
1 | OpenGL中的一个着色器代码片段 |
纹理
在上述提到的布林-冯着色模型中,定义了三个反射系数:
而为了定义着色点的属性,便提出了纹理的概念,使用纹理来记录每个着色点的各种属性,包括材质,颜色等,通常情况下,纹理和贴图等价,但严格意义上来说贴图仅是纹理的一种
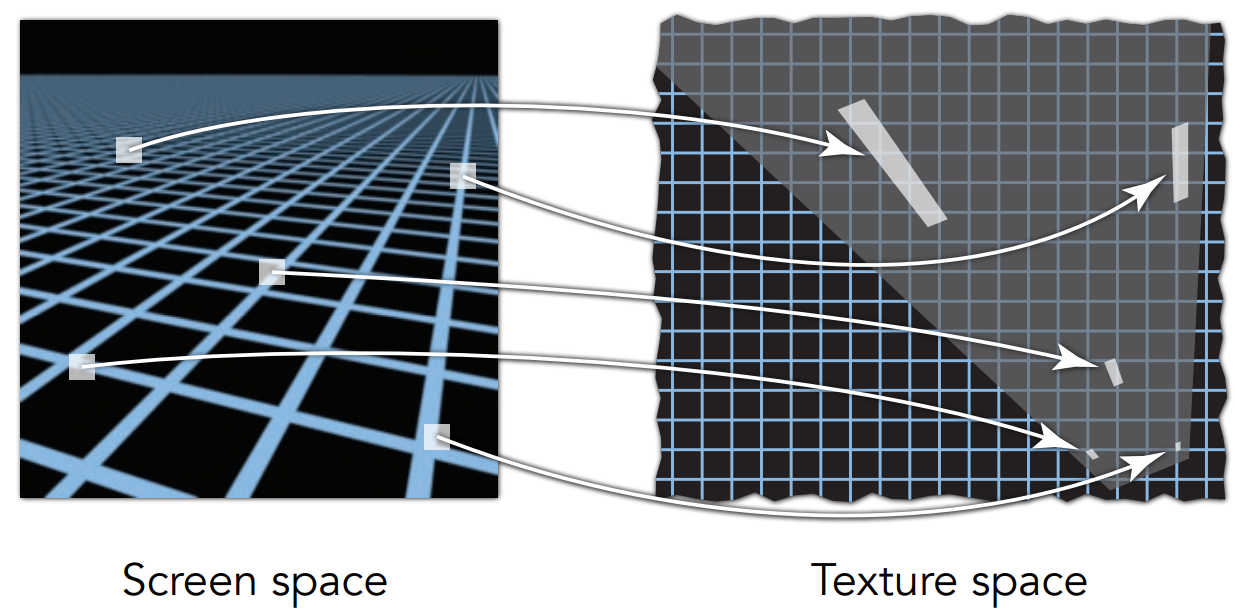
纹理映射
将三位模型上的各个着色点映射到纹理上的过程称为纹理映射
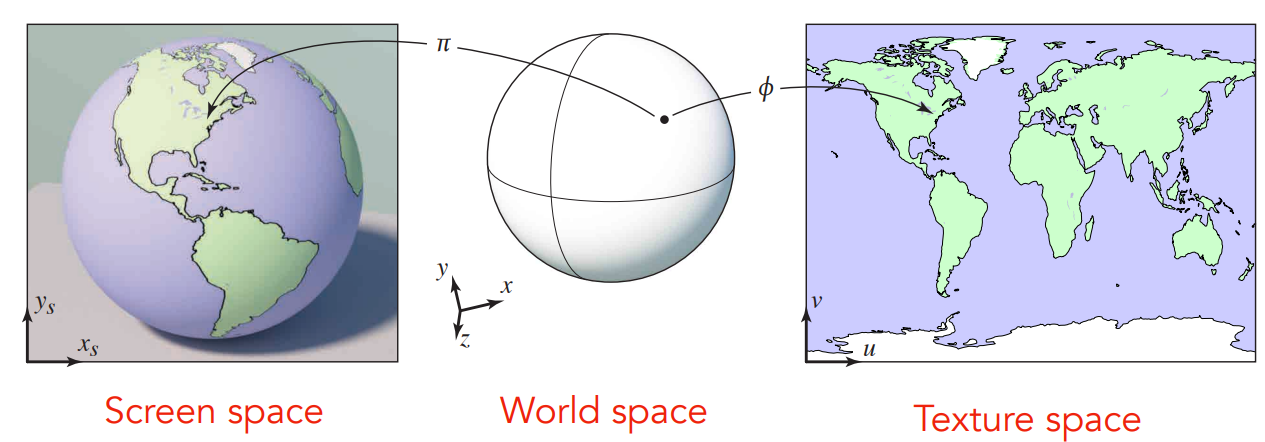
为了方便映射,建立一个纹理坐标系
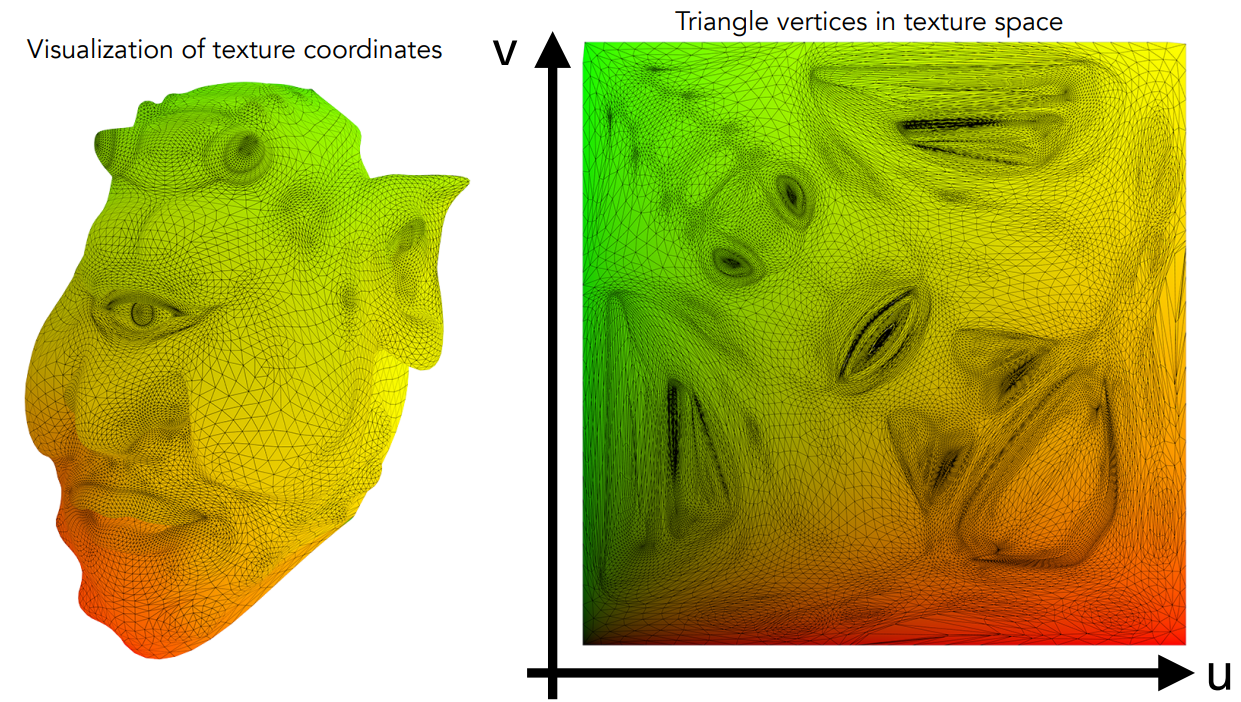
纹理可以被重复使用,通过对一个场景进行一张纹理的重复映射,即可实现整个场景的纹理映射,而纹理与纹理间重复后的自然过渡则是纹理本身的一种属性

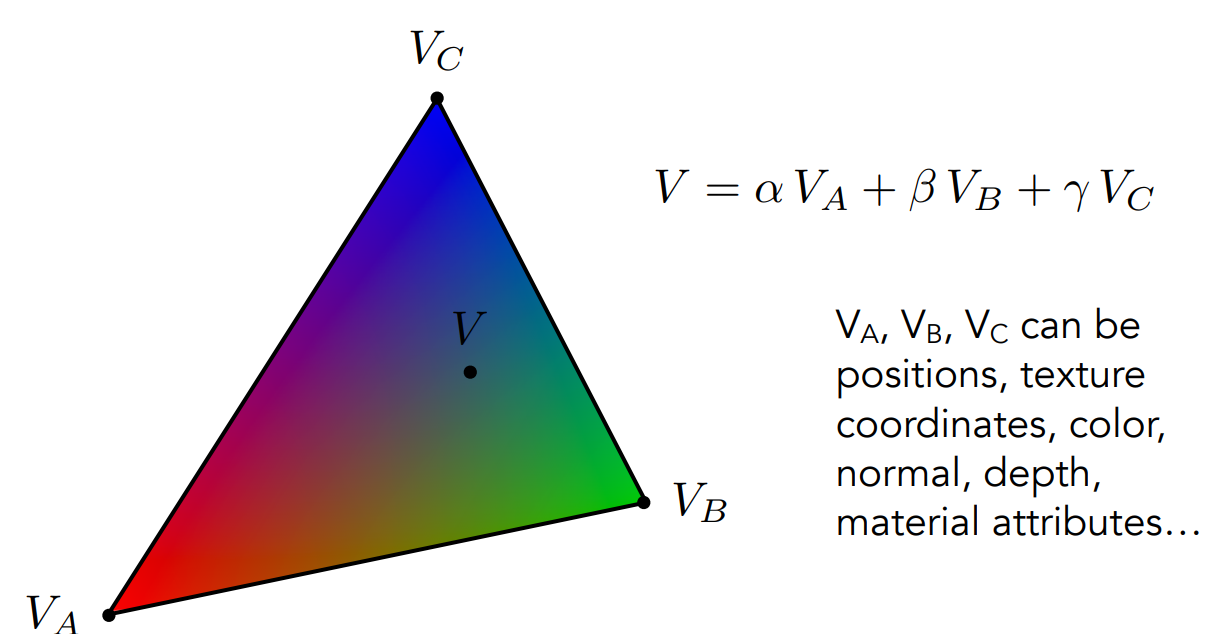
重心插值
在上述的一些操作里大量提到了使用插值的方式来实现不同颜色,属性之间的自然过渡
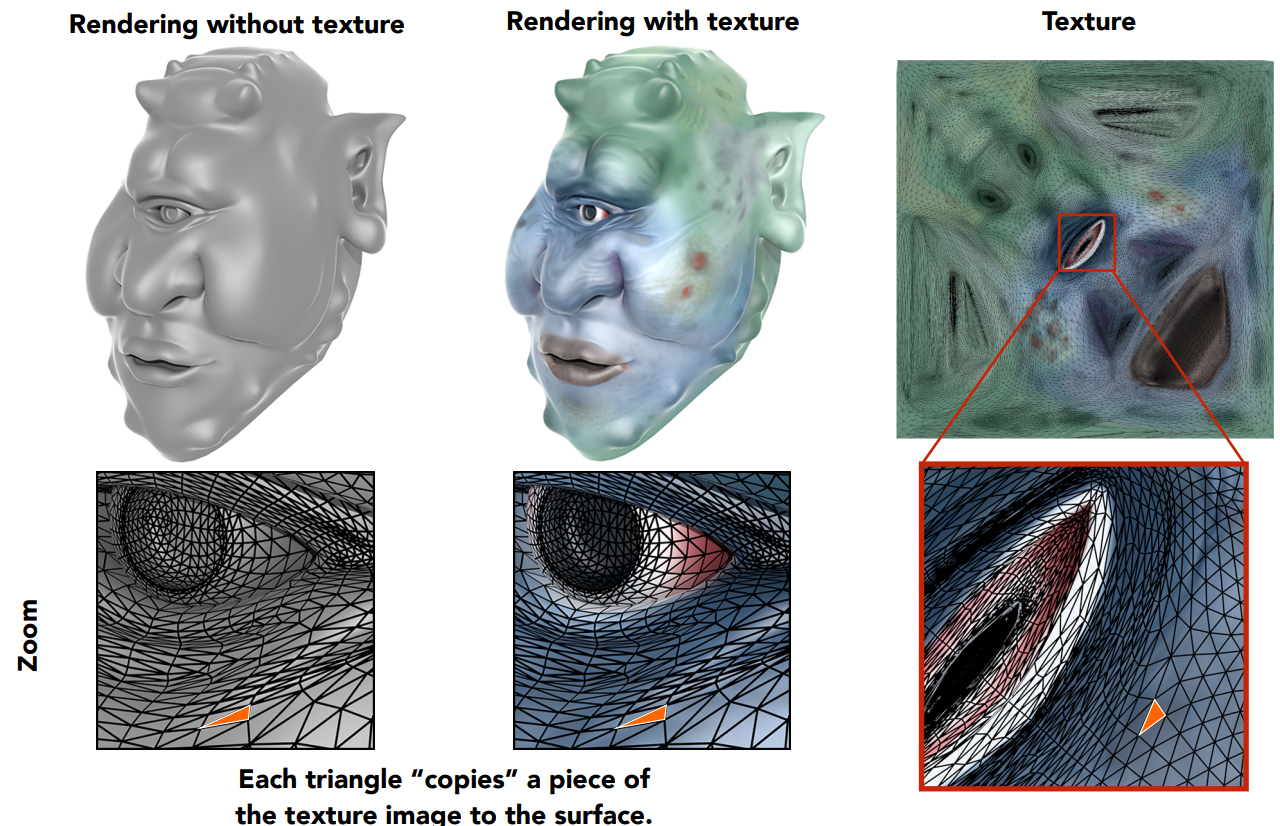
虽然模型和纹理是绑定的,但是绑定是基于顶点实现的。因此在纹理映射中,对于模型三角形的顶点,可以直接使用绑定的纹理坐标找到纹理中对应坐标的属性。但是模型三角形内部的点也需要通过插值的方式来获取它的纹理属性

对任意一个三角形内部的任意一个点

求出这个点的重心坐标后,再通过对顶点的各个属性进行插值,即可得到内部平滑的属性变化
但需要注意的是:在投影时三角形的形状会发生变化,所以在着色应该基于三维空间的坐标计算重心坐标,然后再做插值
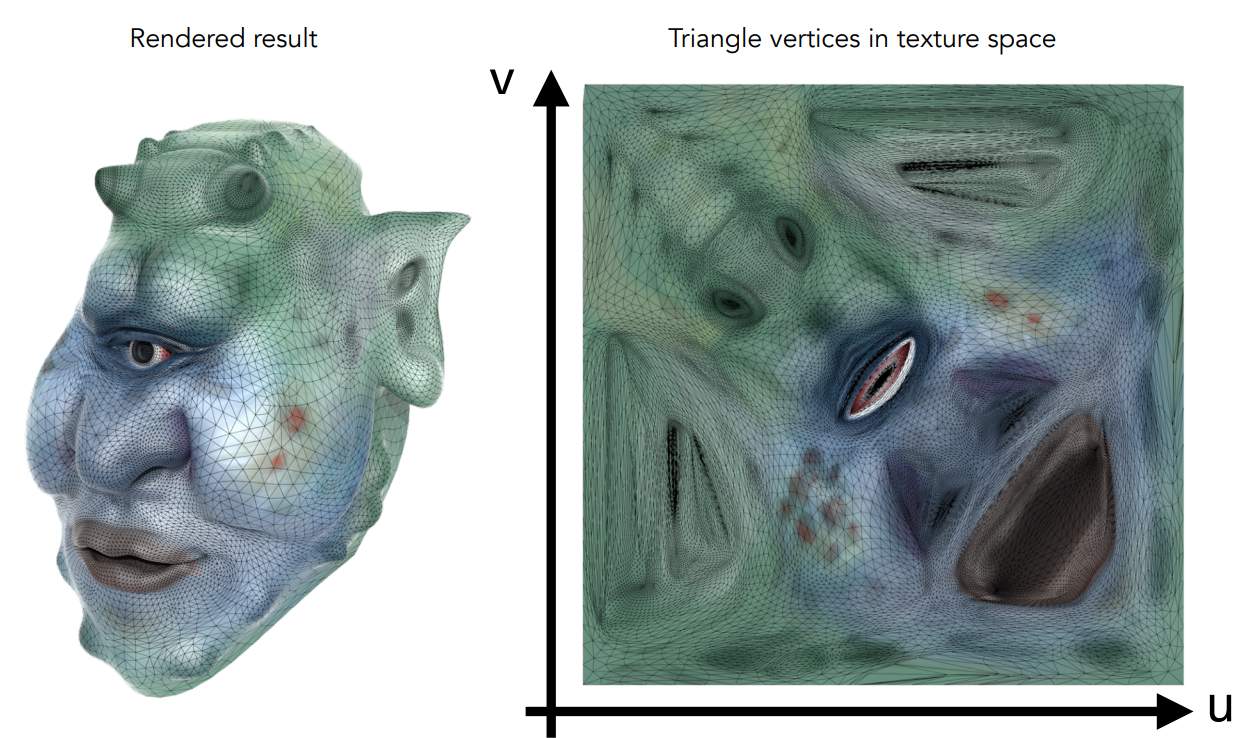
纹理查询
1 | 伪代码实现 |
在光栅化阶段,即当三角形被转换为屏幕上的像素时,每个像素的纹理坐标会通过插值方式在三角形的顶点之间计算出来。此时,可以得到每个像素的屏幕坐标以及对应的纹理坐标
查询的过程:
- 遍历光栅化后得到的每个采样点所对应的屏幕坐标
- 通过像素的屏幕坐标获取该像素所对应的纹理坐标
- 利用纹理坐标在纹理中查找对应属性
- 用纹理的属性来给像素本身着色
这个过程本质上是一个采样的过程,而只要涉及到采样,势必会发生走样的问题,而在纹理查询过程中会有两种情况导致走样
纹理过小引起的走样
当一张纹理的分辨率要小于屏幕显示的分辨率时,那么这张纹理就会被拉伸
如果采取最近采样,容易导致一种情况——多个像素被映射到同一个纹素上(纹理上的最小划分单位),因此就会产生锯齿

而为了解决这个问题,实现像素间的平滑过渡,可以用到双线性插值的方法
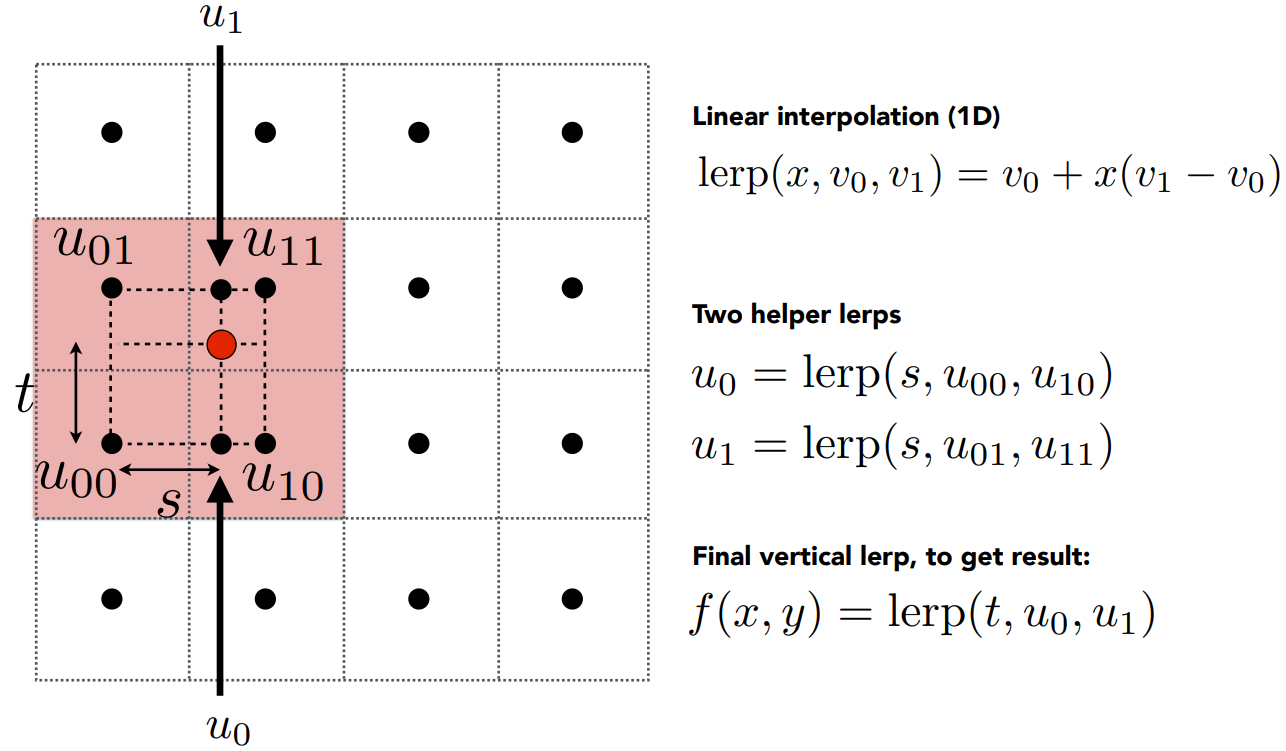
在纹理坐标系中,以与这个像素所对应的点的邻近的四个点重新建立一个
利用这种方法可以有效地解决走样问题
而双三次插值(第三幅图),即使用这个点周围的
纹理过大引起的走样
当纹理过大时,会造成一个像素对应纹理上的一片区域,此时从这个区域中选取一个点来代表整个区域的颜色显然是不合适的
因此就会引起走样的问题,出现摩尔纹等现象
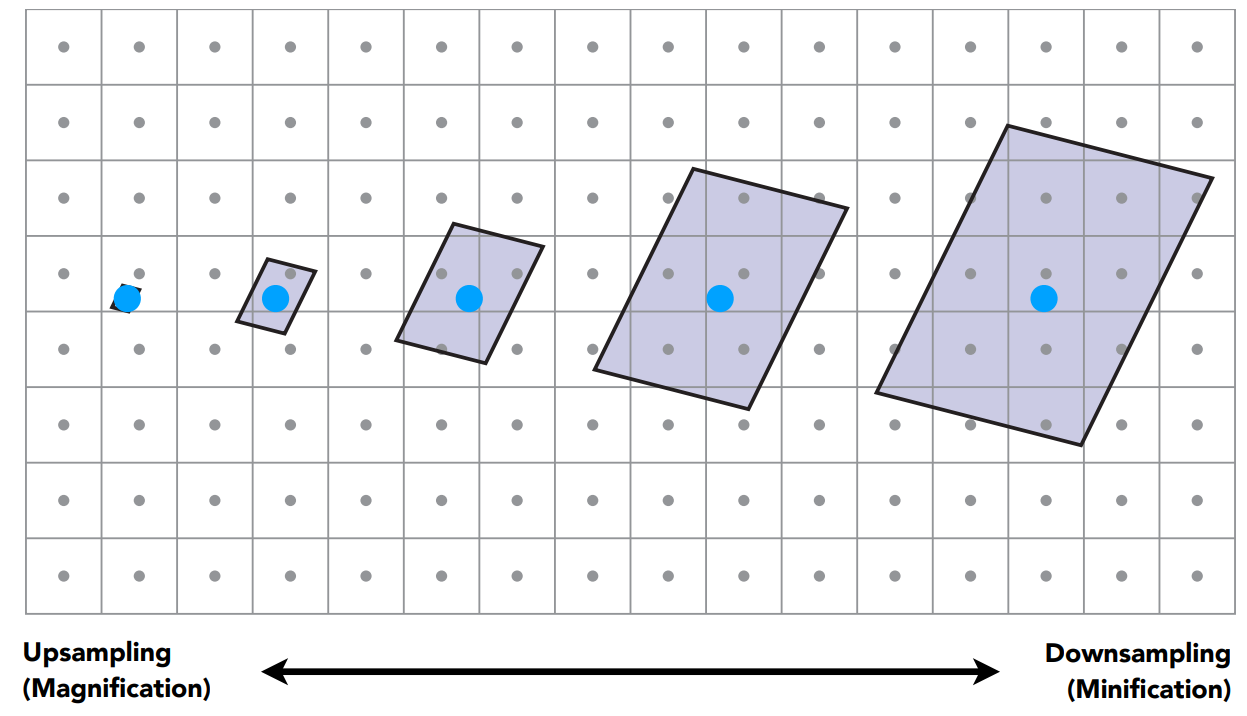

产生这种问题的本质其实是因为采样频率低于信号频率,原因其实与光栅化时类似,因此应用同样的思想,可以得到以下几种解决方式
超采样
增大采样点的个数,将一个像素划分为

由走样产生的原因可以知道,用一个点代表一个区域是不合适的,因此需要一个合理的方式来实现一种范围查询,用这片区域所对应的属性来进行着色

而
每次将纹理的大小变为原来的一半,生成多层的纹理图片,使储存空间变大但操作更快
注意:
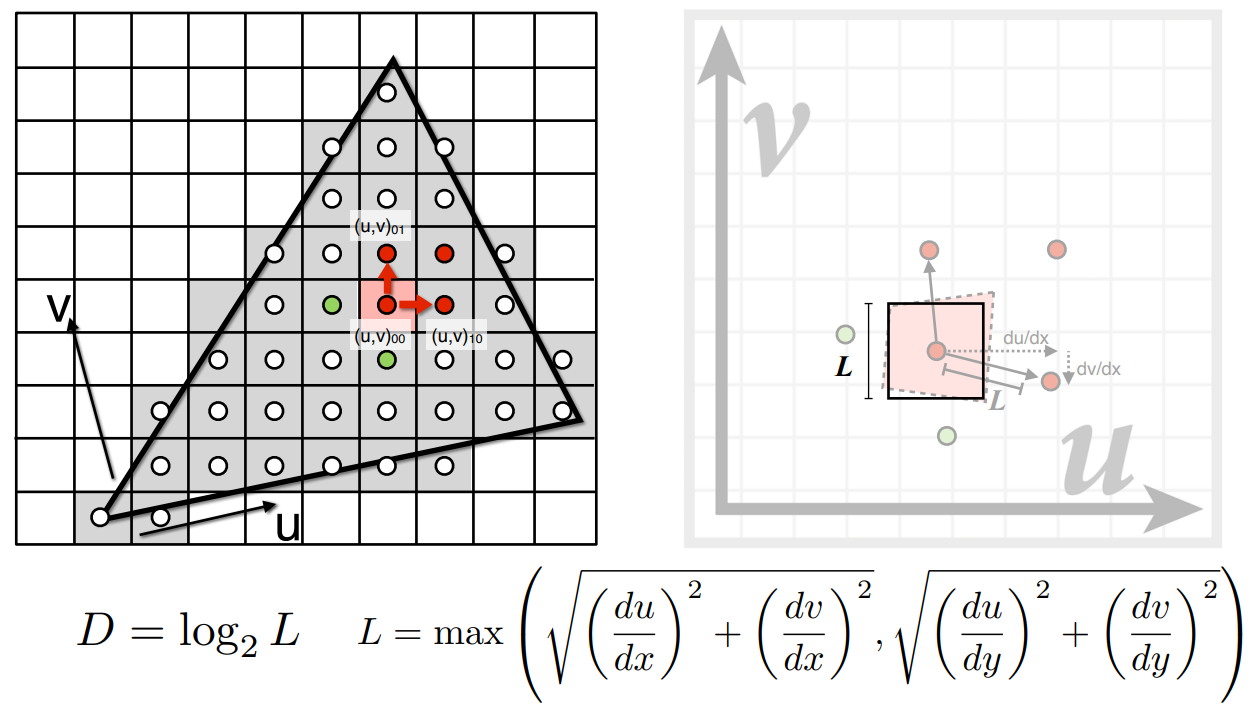
对于屏幕上的一个像素点,考虑其相邻的两个点,获取它们的纹理坐标。根据纹理坐标计算相邻的距离,由此近似得到像素对应的正方形区域,在
但是层级与层级之间会发生突变,这并不是我们想要的

因此通过对层与层之间做一次线性插值,即可实现层与层之间的平滑过渡
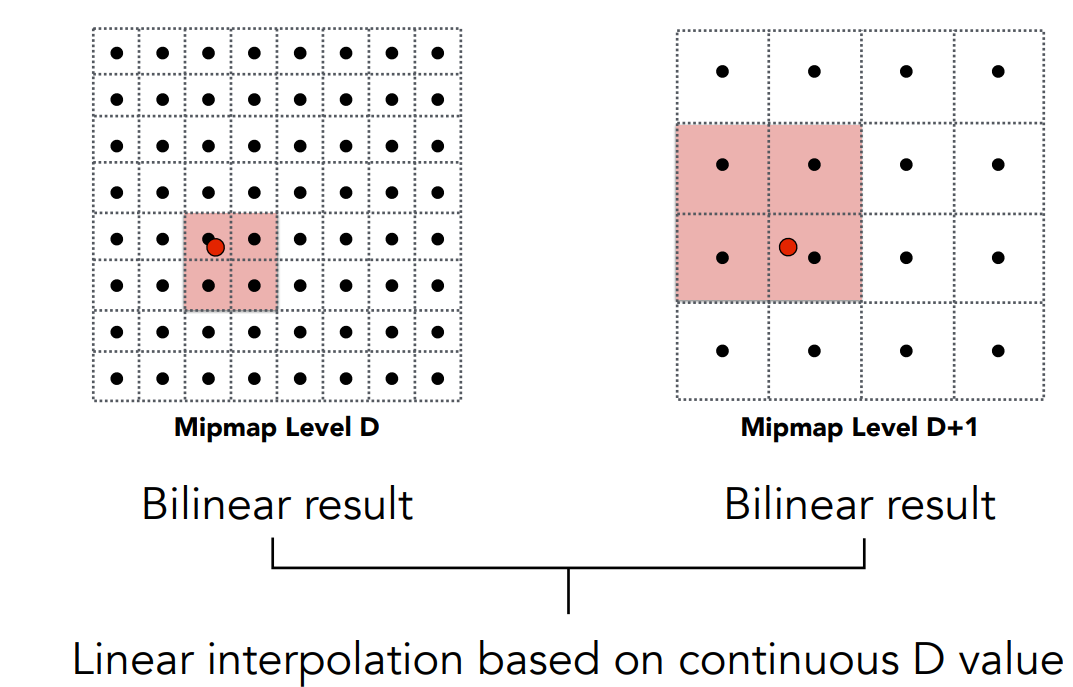

此时来看一下得到的最后效果,发现没有预期的那么好,在远端处的细节都是模糊的

各向异性滤波
思考出现这种结果的原因
用较大的正方形区域代表了原来不大的对应区域,因此出现了走样的情况
此时考虑采用矩形区域来代表其对应区域,这样一种方式称为各向异性滤波

对原来的纹理做切变,长宽不等比例的压缩,生成其他形状的
从上图中可看出,
而各向异性滤波则生成了这样一整张的层级图片
- 对任意不规则的形状采用多个不同大小的椭圆进行逼近覆盖
- 通过
中的不同层级查询 - 多次查询后用加权平均来代表这一个区域的属性
- 性能消耗过大
纹理的应用
实际上,纹理不止可以存储颜色这一种属性,还可以记录如环境光,微几何,法向量,高度偏移等别的属性
环境贴图
光照环境贴图:在渲染过程中预先计算和存储环境光照信息,以提高实时渲染效率和质量

立方体环境贴图:如果在一个房间中,放一个极为光亮的金属球,那么金属球表面所反射出来的图像即为房间中的环境光照,因此可以利用这一点进行纹理的制作,从而制成环境的贴图,将这个金属球映射到一个立方体的六个面并展开,即可得到这样一张贴图,可用于实现镜面反射和环境反射
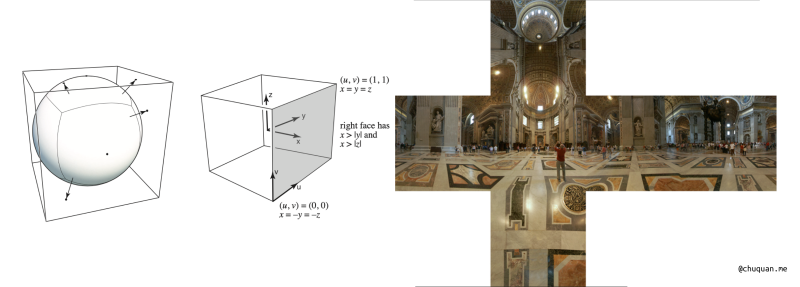
凹凸贴图(法线贴图)
在渲染一个凹凸不平的物体时,如果使用三角形分割表示这个物体画,需要大量的三角形,会产生大量的面数,十分消耗性能,结构也会十分复杂,因此可以采用贴图的方式来实现
定义一张纹理上各个点的相对高度,从而改变法线的高度,导致计算出来的实际渲染效果产生了凹凸不平的视觉错觉
但这种方式本质上并没有改变模型的形状,仅通过光照的计算实现,因此凹凸表面的阴影遮挡实际上无法显示
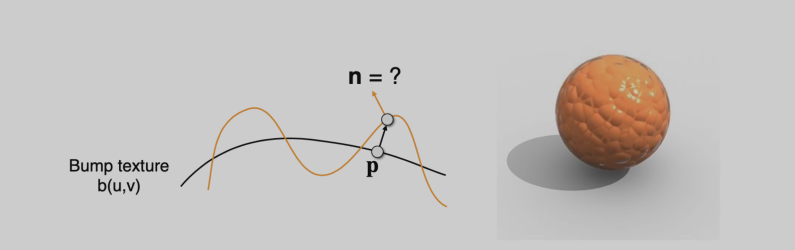
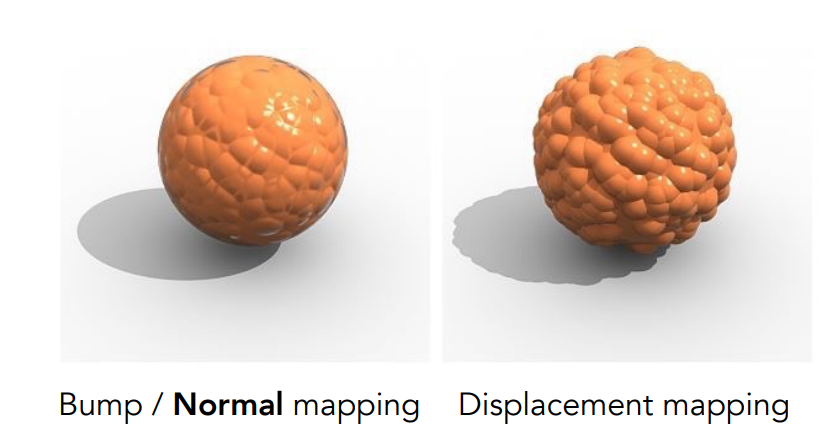
位移贴图
凹凸贴图改变了着色时所使用的法向量,但并没有真正改变模型的形状。而位移贴图则定义了顶点高度的偏移量,改变了模型的形状与其对应的三角形的投影,实现了更逼真的效果,也可以实现凹凸表面的阴影遮挡
3D柏林噪声纹理
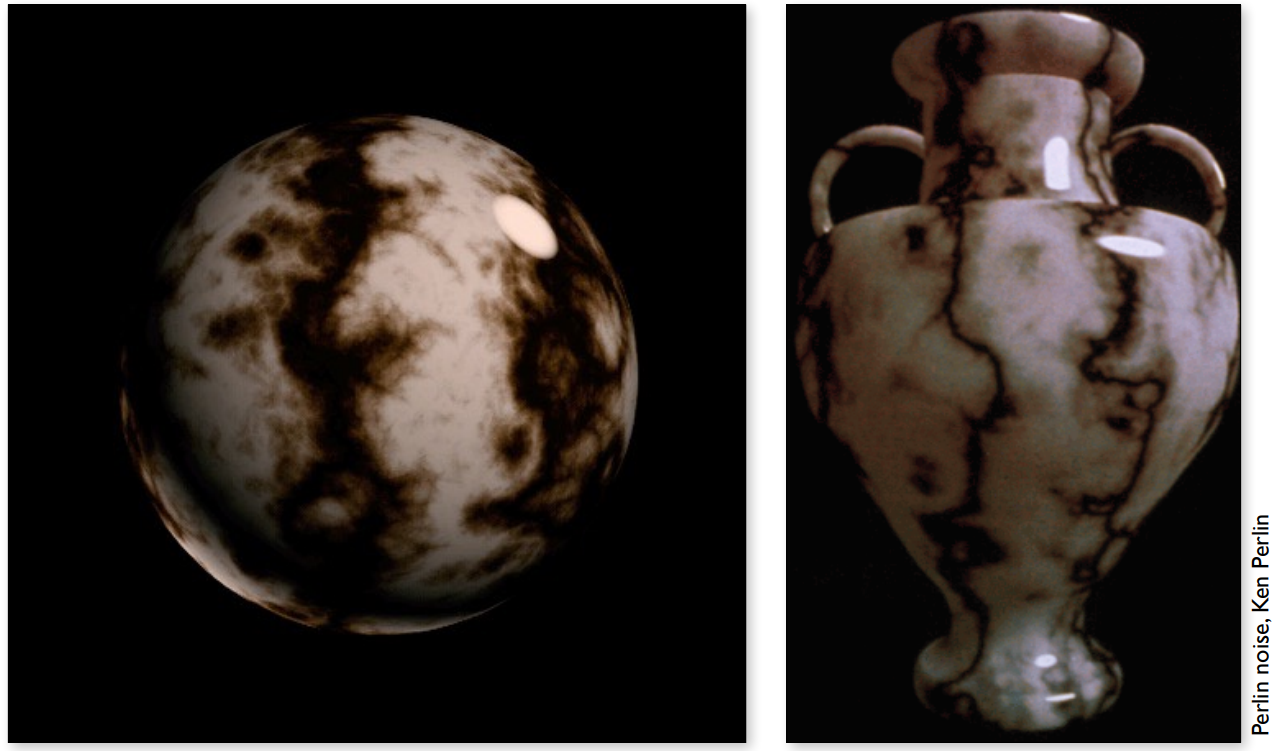
体积渲染