材质与外观
在前面的学习中提到了纹理,在图形学中,不同的材质其实就是不同的外观,本质都是光线在物体表面作用结果,由于材质的不同光线作用后会得到不同的结果,同样的模型会渲染出不同的结果

反射和折射
与光线的作用其实就是折射和反射的组合,下面从折射和反射的角度来看不同的材质与光线是如何作用的
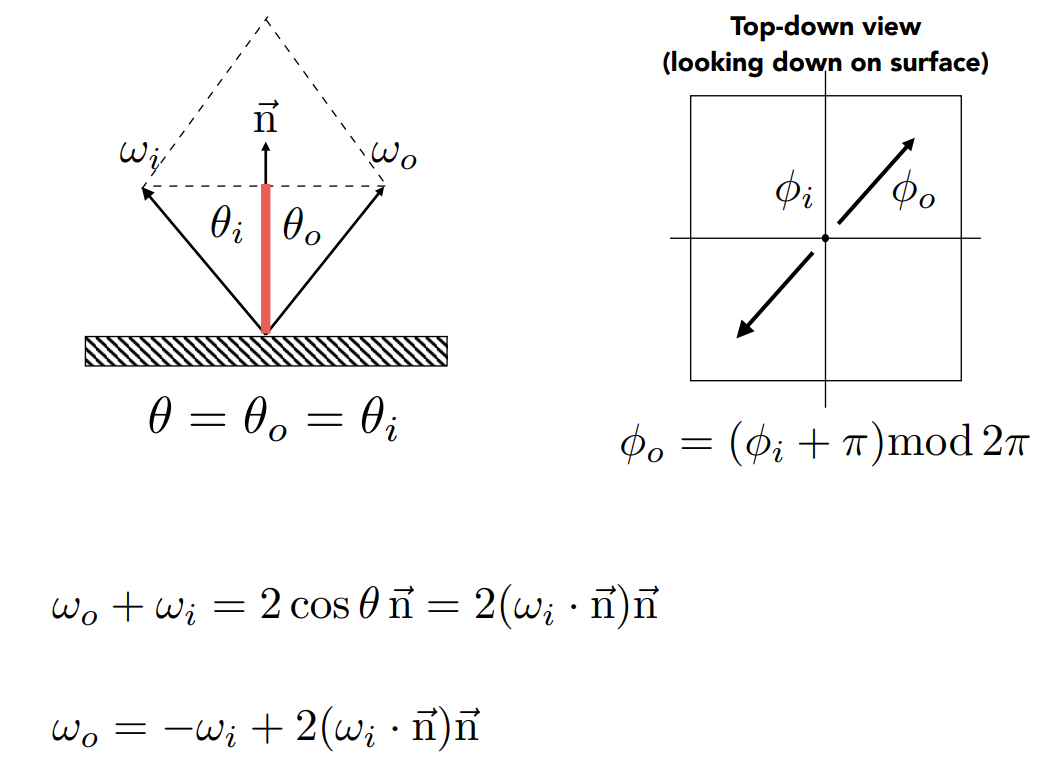
镜面反射
物理意义上的完全反射,入射光方向与法线的夹角=出射光与发现的夹角
将其投影至局部坐标系后(俯视图)入射角和出射角方向相反
折射
物体在不同的介质中传播光线发生偏折的现象,由此有斯涅尔折射定律,同样将其投影到俯视面上
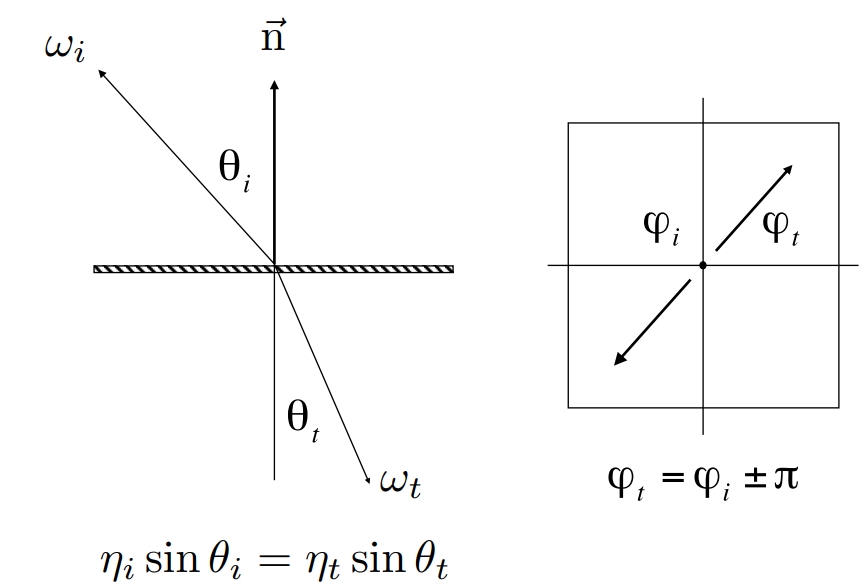
对斯涅尔定律的式子进行变形得到
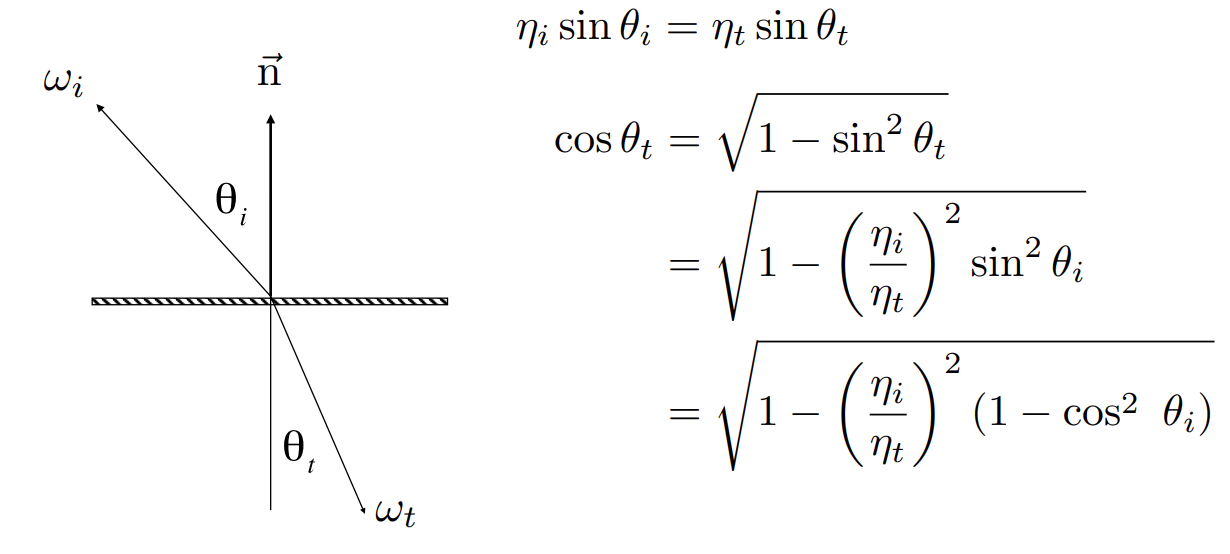
为使这个公式有意义,根号下的式子应该小于
所以这会产生一个有趣的现象,在水底向上看时只能看到一个窗口,称为斯涅尔窗

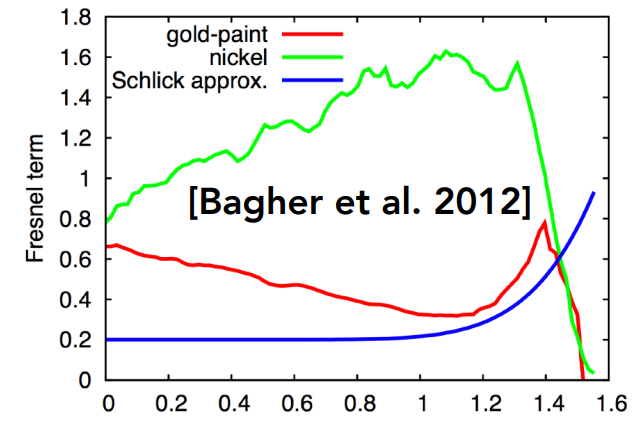
菲涅尔项
在实际生活中会观察到这样一个现象,当观察的角度不同时,物体发生反射的情况不尽相同

而菲涅尔项就是描述这一现象的一个参数
下图是两种不同材质的物体的菲涅尔项
- 电介质
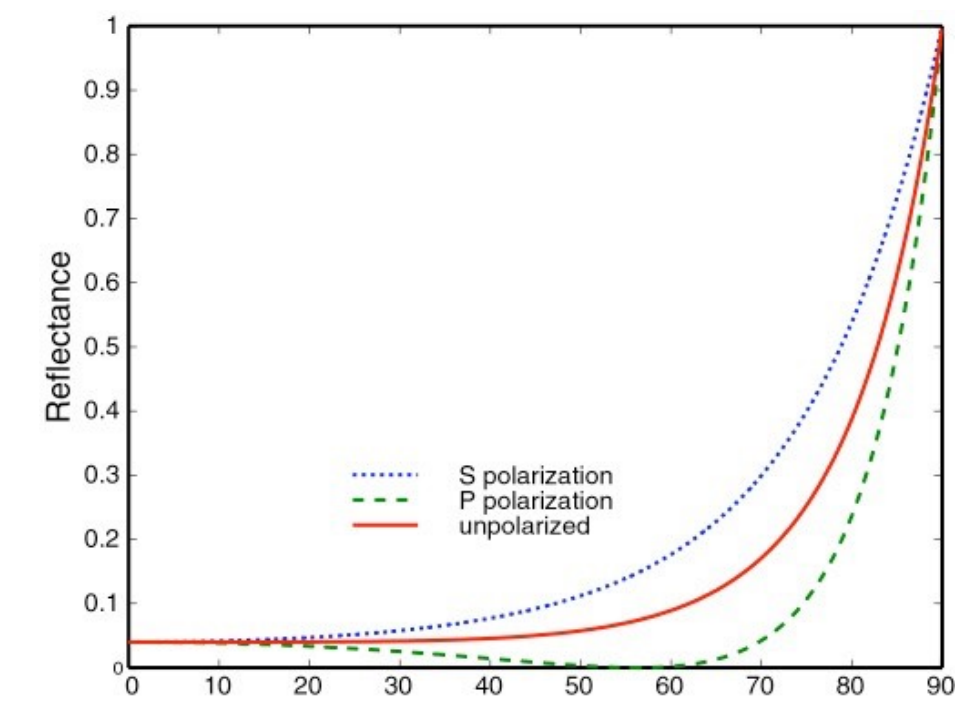
- 导体
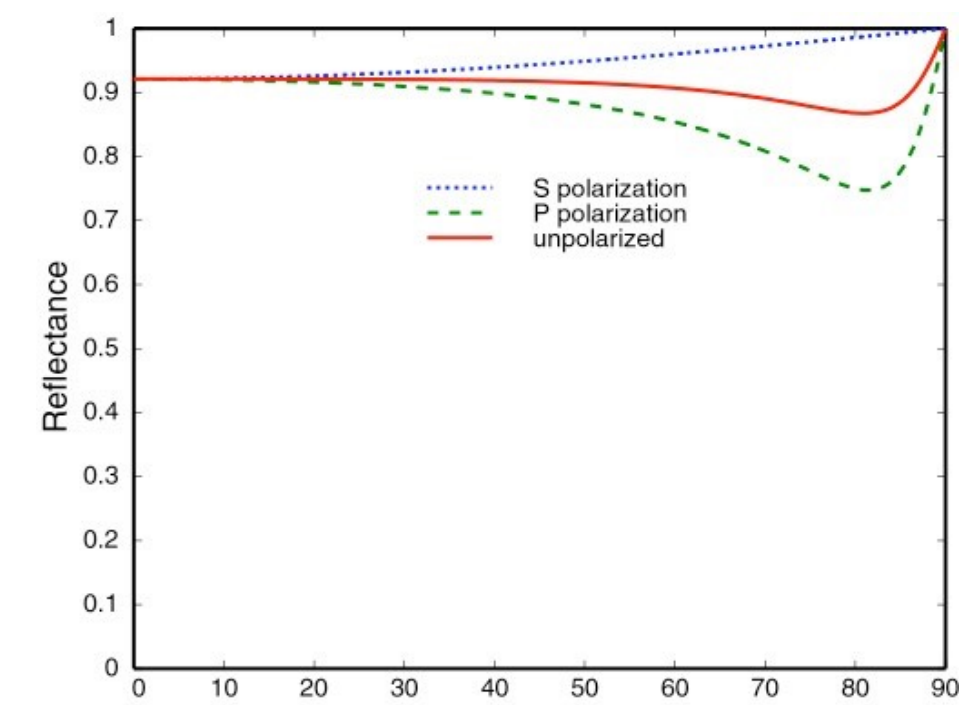
菲涅尔方程:
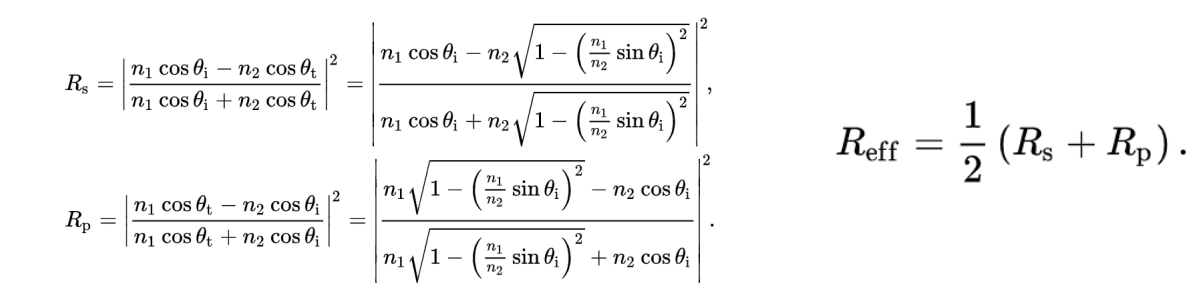
近似公式
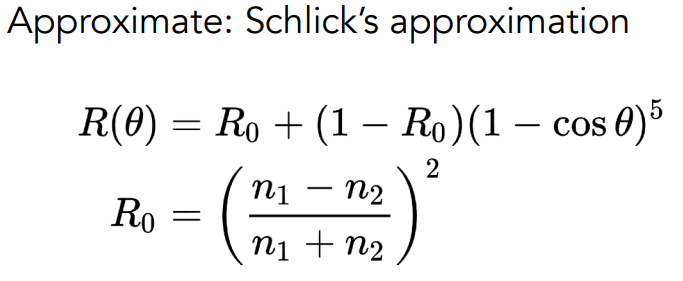
材质
在了解了光线的几种作用后,下面介绍不同的材质与光线之间具体发生什么样的作用
漫反射材质/兰伯特材质
该材质表面主要发生漫反射,在漫反射中光在与物体表面接触后会被均匀地反射到四面八方

假设进来的光也是均匀的,表面不吸收光,由渲染方程,对发生在表面的一个半球进行积分,则可以得到这样一个式子
在假设中出射光的强度与入射光的强度相同,进一步得到:
那么就可以得到漫反射材质的BRDF,且
磨砂材质(Glossy)
如铜等一类较为模糊的镜面反射,发生一种类似于镜面反射的作用,反射方向集中在镜面反射附近的一个小范围

透明材质
这种材质同时发生反射和折射如玻璃,塑料,水等

可以用BSDF来表示这种材质,即将反射与折射相加,BSDF = BRDF + BTDF
微表面材质
当距离一个物体极远来观察这个物体表面时,其实并不能看到表面的具体细节,而是所有这些光产生的总体的一种效果,类似于在一个平面发生的反射

微表面原理
当用一个平面来近似这样一个复杂的表面时,会有这样两种情况
- 微表面法线分布集中——Glossy材质
- 微表面法线分布分散——Diffuse材质
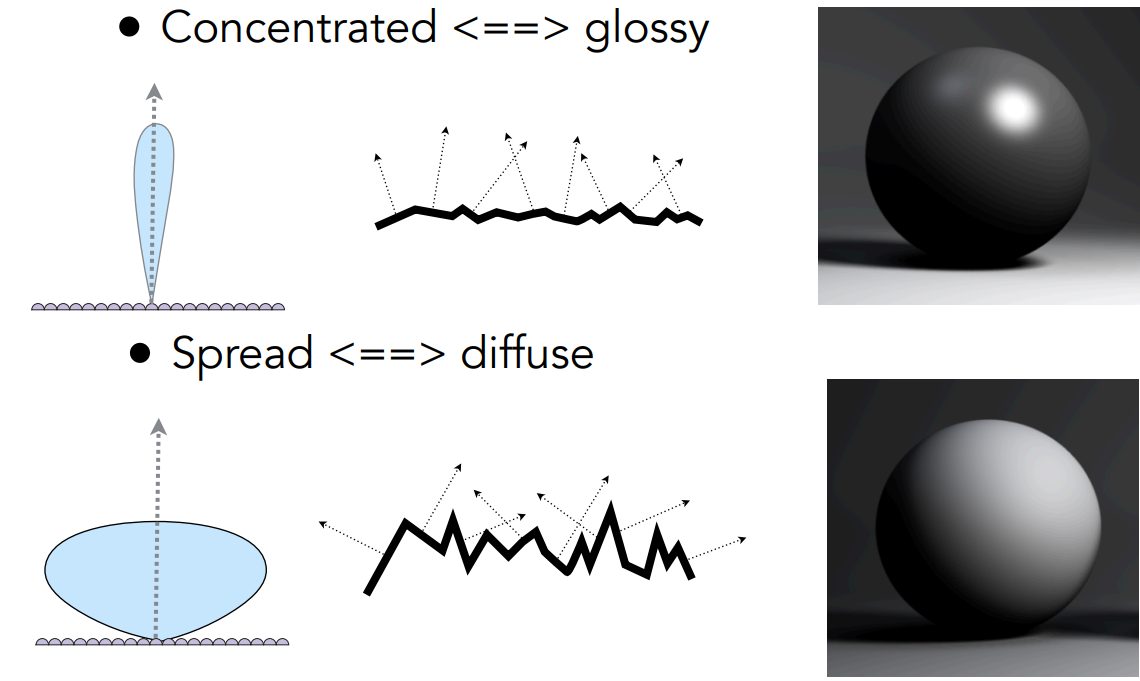
微表面材质的BRDF
微表面材质的BRDF主要由三项构成,物体的菲涅尔项,法线的分布与由物体本身自遮挡而产生的几何项
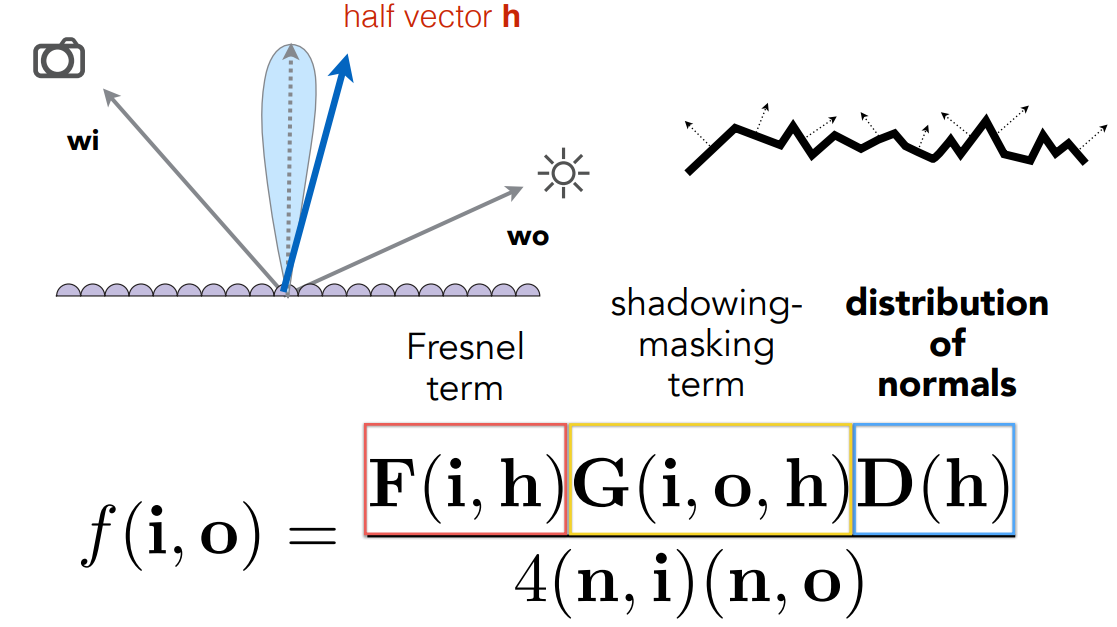
- Fresnel term:不同入射方向带来不同程度的反射,侧重能量。
- distribution of normals:法线分布,表示对于给定方向分布的值是多少。结合半程向量h就可以确定什么样的微表面可以从入射反射到出射(半程向量离法线越近越能反射)。
- shadowing-masking term:几何项,由于自遮挡现象使得有些微表面的作用。当光线几乎平着的打到微表面就容易发生shadow-masking。
在实际应用中,微表面模型有极为广泛的应用,并且有着较好的效果
各向异性/各向同性材质
在前面学习

- 各向同材质:各个方向性质差异不大,大致相同(一般为分布杂乱的材质)
- 各向异材质:各个方向性质差异很大,表现出明显的方向性(一般为规律分布的材质)

对于这一类材质的BRDF,有以下结论:
- 各向同材质:
- 各向异材质:
常见各向异性材质:不锈钢,尼龙,天鹅绒等




BRDF的性质
- 非负性:
- 线性:
- 可逆性:
- 能量守恒:
- 各向同性与各向异性:
(各向同性)
对式子变形:
BRDF的测量
即使有了充足的理论知识对于BRDF进行计算,但是仍然存在不够真实,误差较大的问题,并且BRDF计算起来较麻烦,因此可以考虑在实际情况中测量中一些材质的BRDF,并直接记录在数据库中,直接进行查询
基本原理就是BRDF的定义:让光源打在物体的各个地方然后让相机从各个方向去拍照
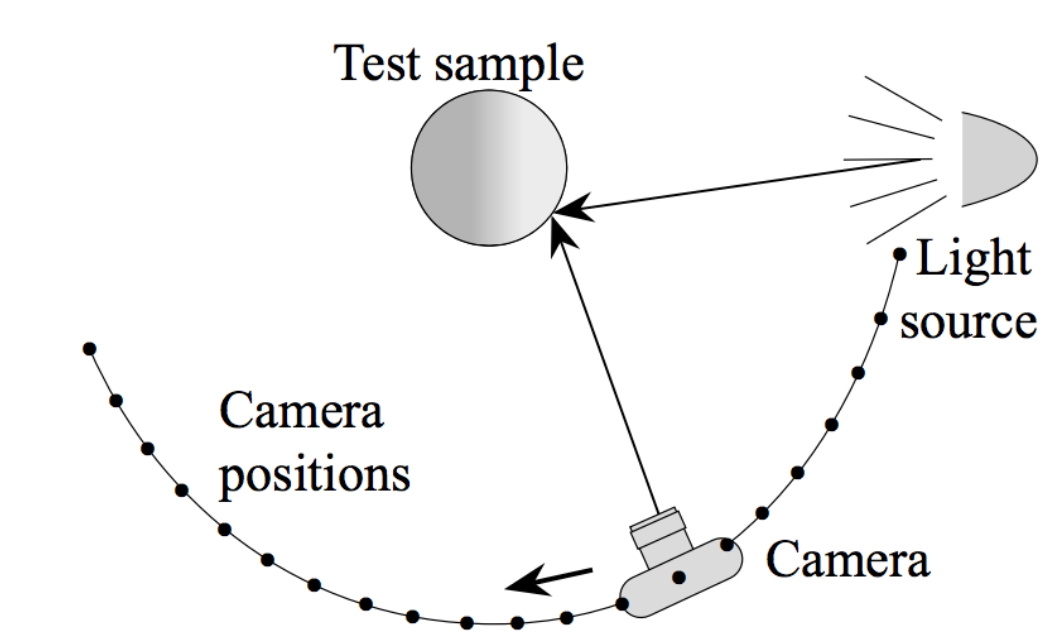

表示BRDF的数据结构也需要有一些良好的性质:
- 紧凑的表示
- 测量数据的准确表示
- 对随意一对方向的高效预测
- 可用于重要性抽样的良好分布
Tabular Representation表格表示是其中一种,将规则空间采样后存储在三维数组
材质库:MERL BRDF
