2维坐标的线性变换
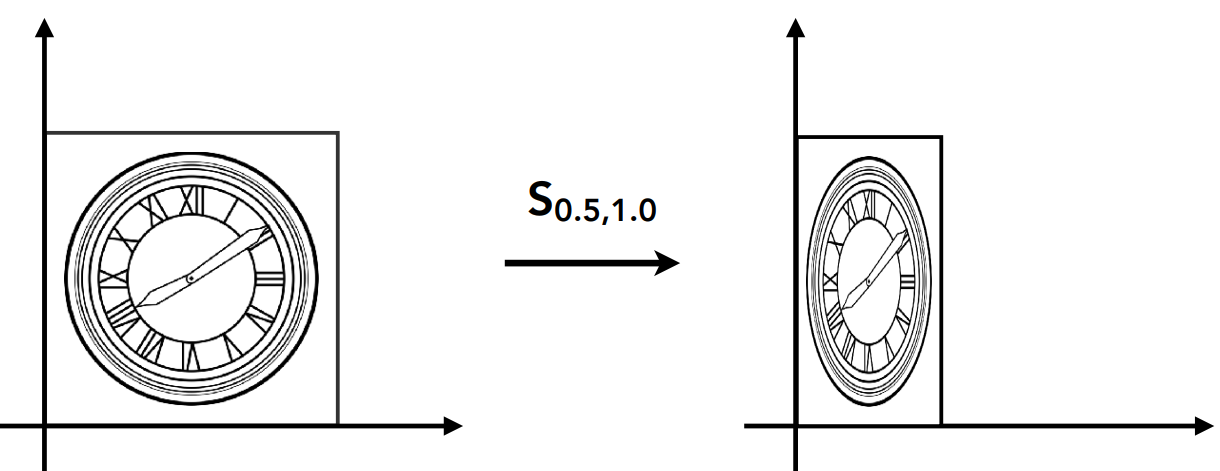
缩放
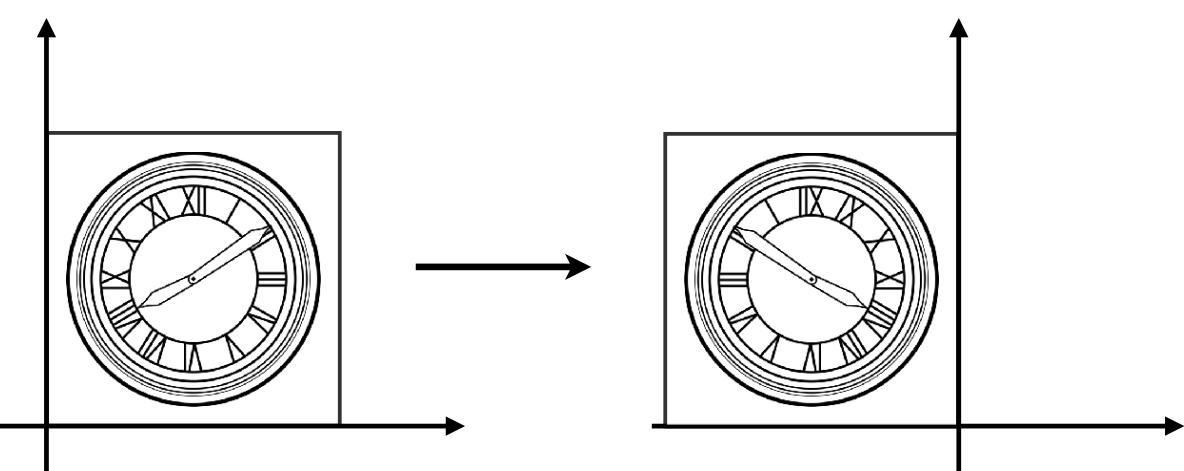
对称
切变
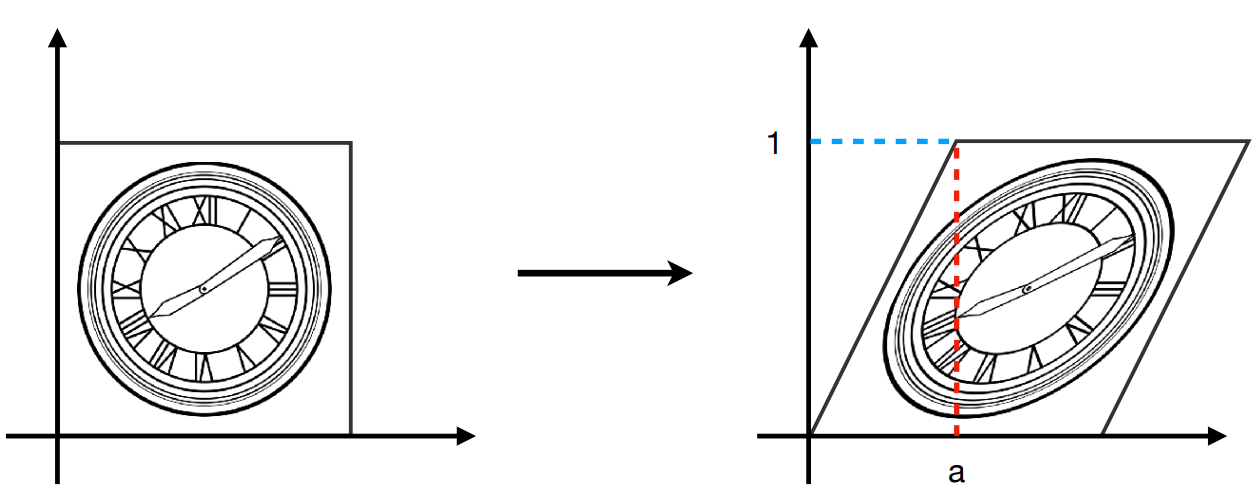
注意:将图片y轴标准化为1后再乘上对应的矩阵
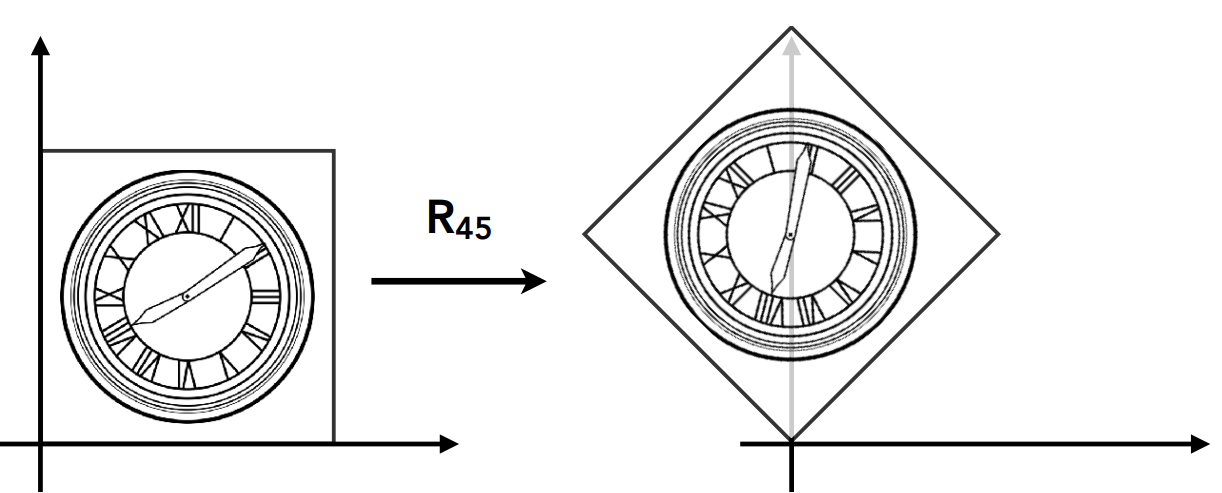
旋转(绕原点且为逆时针)
2维坐标的仿射变换
齐次坐标
拓展:如果
平移
仿射变换
仿射变换 = 线性变换 + 平移
齐次坐标下:
复杂变换
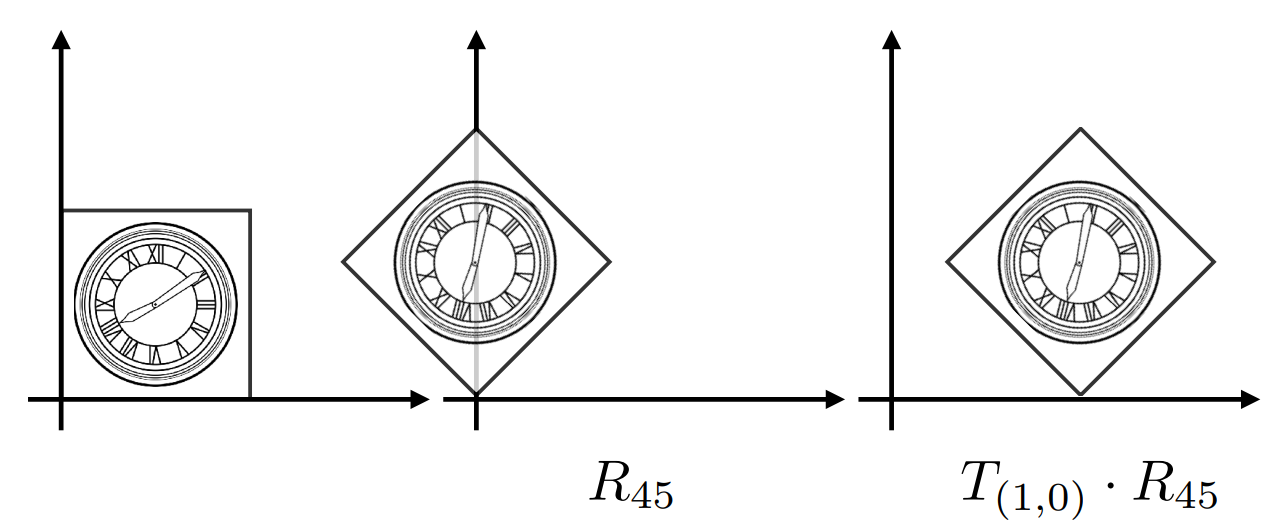
注意顺序
当进行一系列的仿射变换,其对应的齐次左边下的矩阵分别为:
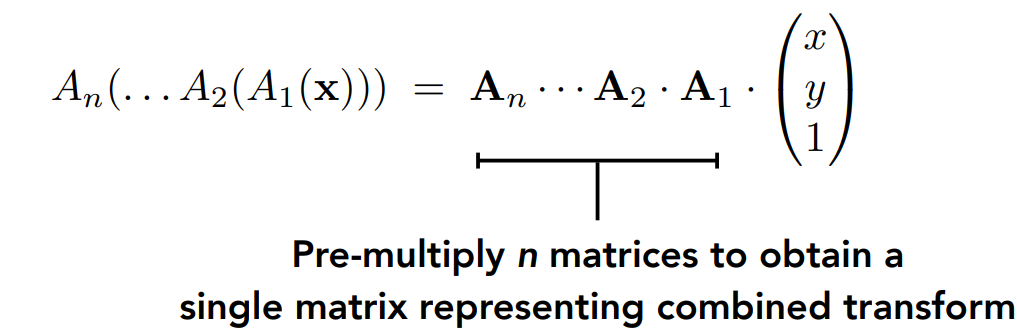
可以先做
对于绕任意一点旋转,可以先将其平移至原点,旋转后再平移回原位置:

3维坐标变换
3维的齐次化坐标
罗德里格斯旋转公式
在
罗德里根旋转公式:
公式推导:
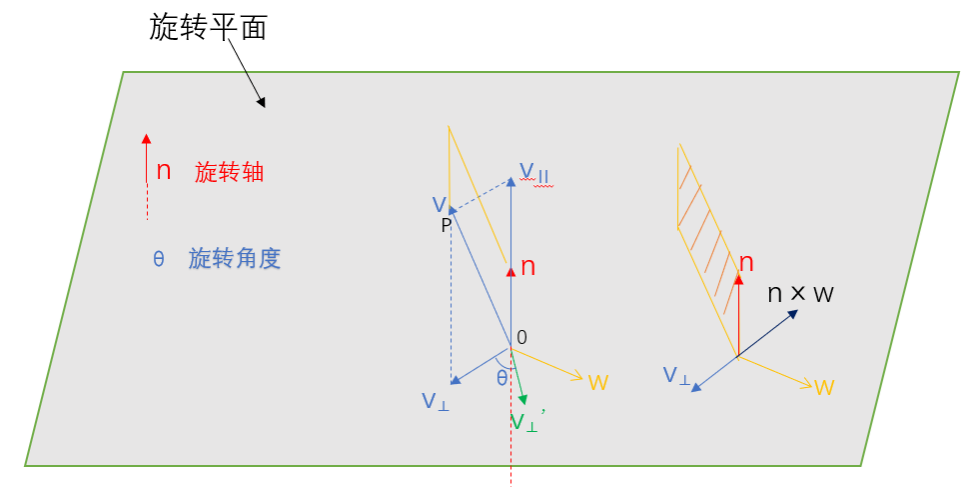
对于空间中任意向量
其旋转后所得到的向量:
以
旋转后
观测变换
视图变换
如何拍一张照片:
- 找一个地方让人们站过去(模型变换)
- 找一个位置放相机(视图变换)
- 摆造型(投影变换)
先定义三个方向:
- 相机的位置为
- 相机面朝的方向为
- 相机朝上的方向为
相机与物体的相对位置始终是不变的,所以我们可以将相机平移至原点,以相机所在位置建系

以此建系后:相机朝上的方向为
接下来对相机平移至原点,坐标轴转到指定位置做变换:
- 先平移至原点
- 将
旋转至 轴方向 - 将
旋转至 方向 - 将
旋转至 方向
则可得:
易知
考虑先求其逆变换
投影变换
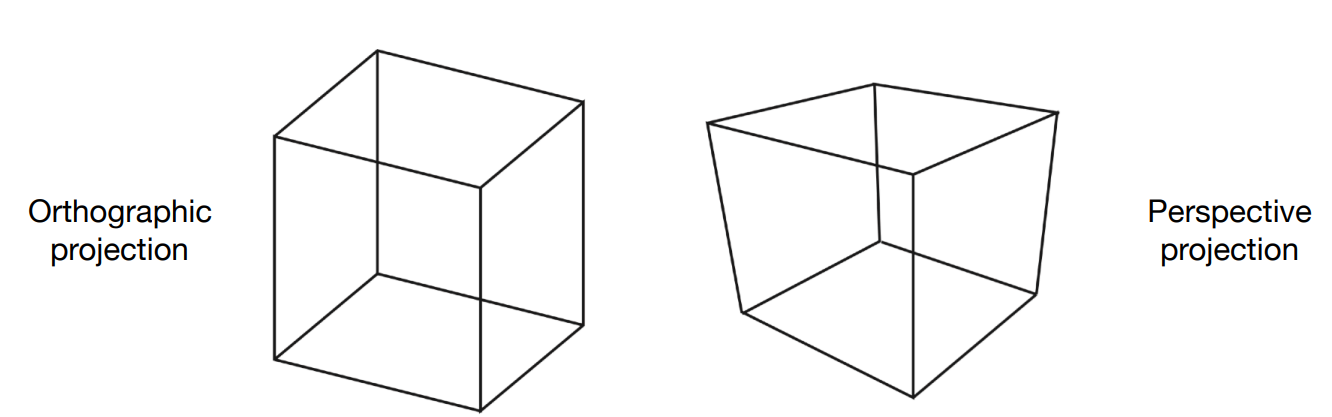
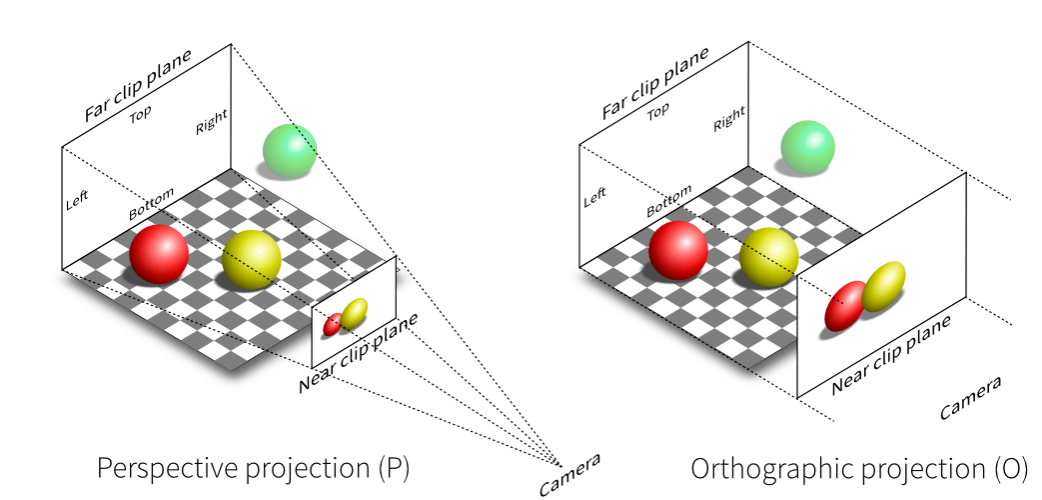
也即有无影消点的区别
正交变换
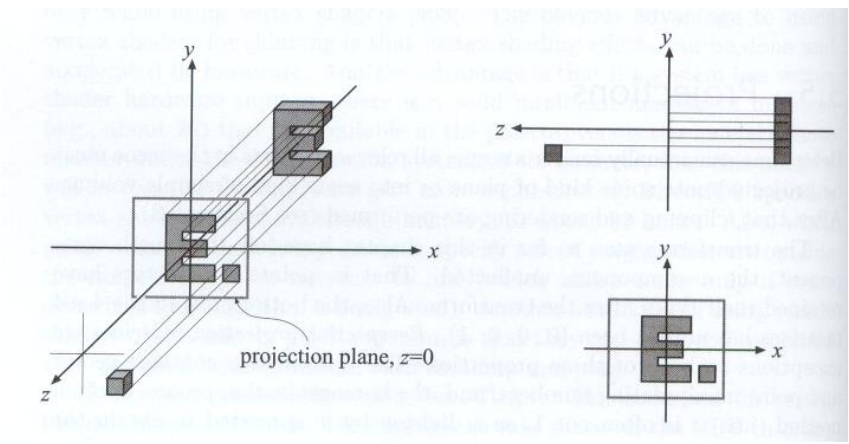
一种简单的方式就是将相机放在原点,面朝
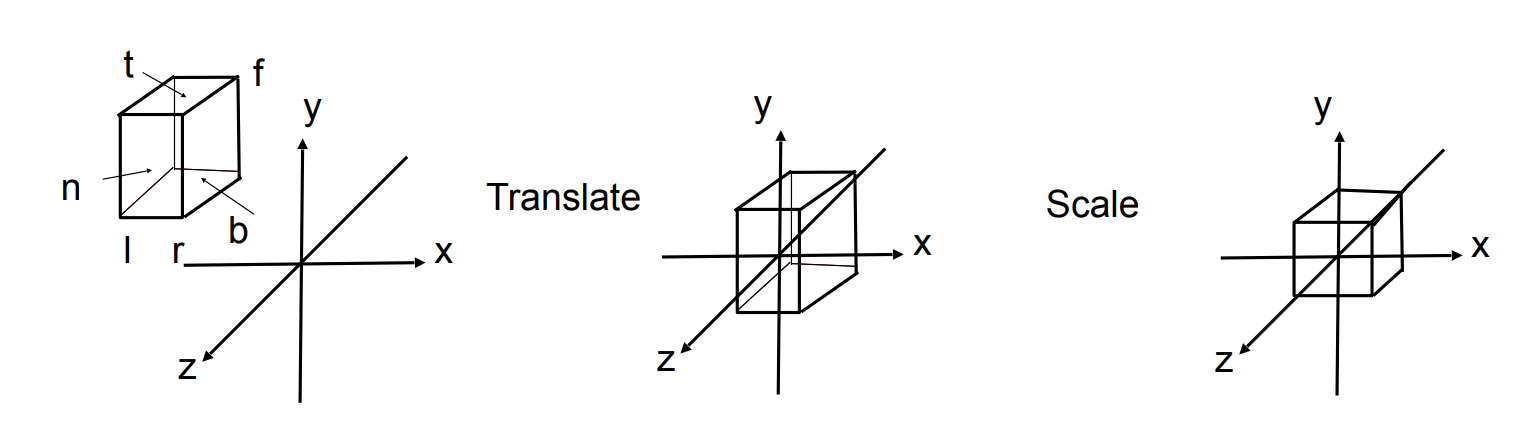
对于正交投影,其观测空间为一个
为了方便计算,将这个长方体的观测空间统一正则化为一个
这个正则化的变换矩阵为:
注意:在右手系下
又物体与相机的相对位置不变,对空间中所有物体进行同样的变换即可
透视变换
考虑这一变换过程,可以分两步:
- 将透视变换对应的台体通过变换转化到正交变换的立方体上
- 进行正交变换
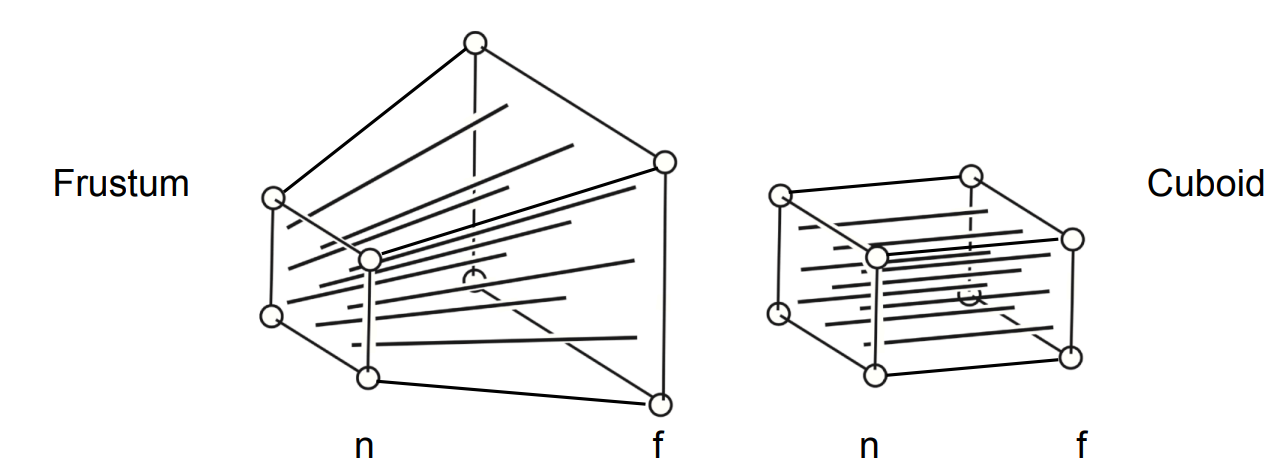
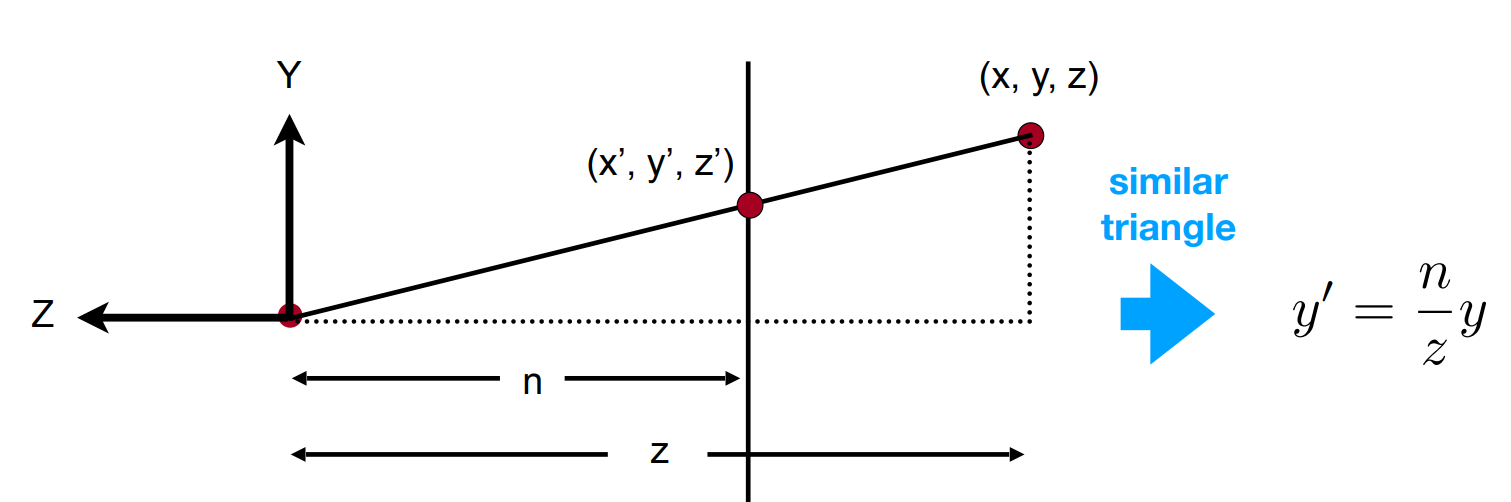
对任意一个点进行上述操作后可得:
易得矩阵
经过变换后有两个性质:
- 近平面上的点
- 原平面上的点
取两个特殊点:
则有:
解方程组:
求得矩阵:
那么最后我们将所有的物体乘上
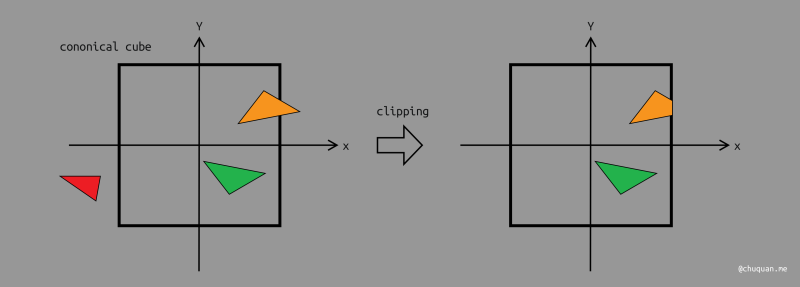
裁剪
无论是正交投影还是透视投影,我们都将观测空间转换成了一个规范立方体,同时将转换矩阵应用到空间中的所有物体中。
之后,我们就可以通过规范立方体对空间进行裁剪,只保留规范立方体内的物体,如下所示。很显然,只有在规范立方体中的部分才是我们可以看见的部分。
视口变换
将我们所正则化后的
即将
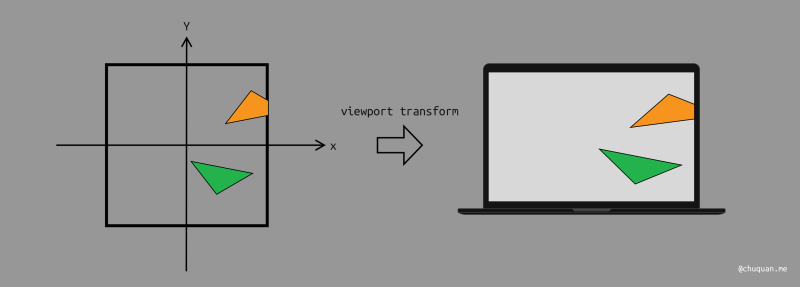
最后得到视口变换的矩阵:
即:切变+平移